Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 28. 03. 2013 16:17 — Editoval kajman (28. 03. 2013 16:25)
Elipsa
Zadání:
Napište rovnici elipsy, je-li hlavní osa rovnoběžná
a) s osou x
b) s osou y
a je-li S[-2;3], b =3, a jeden její bod X[2;4,8].
Pěkné odpoledne.
Jaksi jsem se zde zasekl.. 
Potřebuji jen nakoupnout.. Bod S dosadím za m,n, b=3 za béčko a bod X za x a y?
Děkuji Vám.
Kajman
Offline
- (téma jako nevyřešené označil(a) kajman)
#2 28. 03. 2013 16:19 Příspěvek uživatele kajman byl skryt uživatelem kajman.
#4 28. 03. 2013 16:55
Re: Elipsa
↑ kajman:
Ahoj..
Rovnice elipsy je 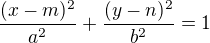
Je to přesně jak píšeš, bod S dosadíš za m,n, b=3, a bod X za x,y (jenom tady máš asi chybu, souřadnice u bodu X musí být zadané jen dvě).
Pokud hlavní osa elipsy je rovnoběžná s osou y, tak se to projeví v její rovnici tak, že větší číslo bude ve zlomku, kde je v čitateli (y-n)^2.
Offline


![kopírovat do textarea $S[m;n]$](/mathtex/c2/c28288e48c15ffa3f74c36c61a41d426.gif)
![kopírovat do textarea $X [x;y]$](/mathtex/e0/e0bbf081b68e5e676454c327f2574f3f.gif) a
a  Dopočítáš
Dopočítáš  .
.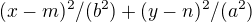 a dále je to stejné.
a dále je to stejné.