Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 07. 04. 2013 15:39
Rovnice v oboru C
Ahoj, tak trochu si nejsem jistý, jak se dál postupuje ve výpočtu.
Mám řešit rovnici v C:
Pokud budu uvažovat komplexní číslo 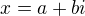 , tak si to můžu přepsat jako:
, tak si to můžu přepsat jako: (1)
(1)
Protože  je komplexní číslo a
je komplexní číslo a  je reálné.
je reálné.
Pak dostávám:
Pak jsem zjistil, že se postupuje tak, že si rozdělím rovnici na část reálnou a imaginární.
Imaginární
Reálná
Mám to zatím dobře nebo už někde dělám chybu? Díky.
Offline
- (téma jako vyřešené označil(a) bejf)
#3 07. 04. 2013 16:05 Příspěvek uživatele LukasM byl skryt uživatelem LukasM. Důvod: zavádějící blbost
#4 07. 04. 2013 16:11 — Editoval bejf (07. 04. 2013 16:15)
Re: Rovnice v oboru C
↑ byk7:
Dobře.
Z imaginární části dostanu tedy 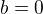 a dosadím do reálné části.
a dosadím do reálné části.
Ta mi vyjde:
Odsud: nebo
nebo 
Tedy 

Kořen a=0 platí.
Kořen a=1 neplatí.
Kořen a=-1 neplatí.
Takže když teď dosadím 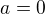 do
do 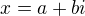 a
a  , tak dostanu:
, tak dostanu: odsud
odsud 

Odsud 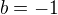
Takže  .
.
Tedy  . Správně?
. Správně?
Offline
#5 07. 04. 2013 16:24 — Editoval LukasM (07. 04. 2013 16:25)
Re: Rovnice v oboru C
↑ bejf:
Řešení je snad dobře, ale ten postup mi přijde takový všelijaký. Jak třeba z  plyne b=1? Navíc když jsi na samém začátku předpokládal, že b=0? (Z "im. části" mj. neplyne že b=0, plyne z ní, že a nebo b je nulové. Je potřeba zkusit obě možnosti.)
plyne b=1? Navíc když jsi na samém začátku předpokládal, že b=0? (Z "im. části" mj. neplyne že b=0, plyne z ní, že a nebo b je nulové. Je potřeba zkusit obě možnosti.)
To řešení se různě větví, a ty to minimálně špatně popisuješ. Ale myslíš to možná dobře.
Offline
#7 07. 04. 2013 17:32
Re: Rovnice v oboru C
↑ bejf:
Takže "učesané" by to mělo být nějak takto:
Z 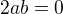 plyne
plyne
a) 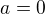 nebo b)
nebo b) 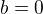
a) dosazením do  dostáváš
dostáváš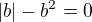
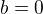 nebo
nebo 
b) doszením
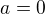
řešení: 


varianta b) je opakováním první varianty a).
Pořádek je pro blbce, inteligent zvládá chaos!
Offline
#8 07. 04. 2013 18:07
Re: Rovnice v oboru C
↑ zdenek1:
Jo tak už mi asi svitlo. :-)
Vyjde mi tedy 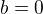 nebo
nebo  a to dosadím pro zkoušku ještě do
a to dosadím pro zkoušku ještě do 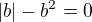 -> při všech třech kořeny dávají platnou rovnost.
-> při všech třech kořeny dávají platnou rovnost.
Pak u b) mi vyjde taky 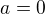 nebo
nebo 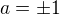 a to dosadím pro zkoušku zas do
a to dosadím pro zkoušku zas do  -> u těchto kořenů splňuje rovnost jen
-> u těchto kořenů splňuje rovnost jen 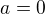
Takže proto má rovnice celkem ty tři kořeny, jak jsi psal. :-)
Offline
#9 08. 04. 2013 09:34
Re: Rovnice v oboru C
↑ bejf:
Ano. Jen doplním, že tu zkoušku netřeba dělat. Stačí si uvědomit, jak že se to řeší rovnice s abs. hodnotou. je pro a>=0, ekvivalentní s
je pro a>=0, ekvivalentní s  - takže když z této upravené rovnice vyjde kořen, který je záporný, pak není řešením původní rovnice. Všechny nezáporné už jsou. Obdobně pro a<=0 je ta rovnice ekv. s
- takže když z této upravené rovnice vyjde kořen, který je záporný, pak není řešením původní rovnice. Všechny nezáporné už jsou. Obdobně pro a<=0 je ta rovnice ekv. s  (protože pokud je a záporné, tak mu abs. hodnota změní znaménko). Takže když z této rovnice vyjde kladný kořen, není řešením původní rovnice. Nekladné kořeny ano.
(protože pokud je a záporné, tak mu abs. hodnota změní znaménko). Takže když z této rovnice vyjde kladný kořen, není řešením původní rovnice. Nekladné kořeny ano.
Zkouška samozřejmě udělá stejnou službu, ale je dobré si uvědomit proč se to vlastně takhle řeší.
Offline
#11 08. 04. 2013 10:40
Re: Rovnice v oboru C
↑ bejf:
Zkusme to ještě jinak.
1) Snadno nahlédneme, že rovnici
(1) 
řeší 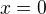 .
.
2) Hledejme nenulové řešení rovnice (1). To se dá vyjádřit v goniometrickém tvaru  ,
,
kde  ,
,  . Dosazením do (1) a s použitím Moivreovy věty máme
. Dosazením do (1) a s použitím Moivreovy věty máme
![kopírovat do textarea $[r(\cos\xi + \mathrm{i} \sin\xi)]^2+ r=0$](/mathtex/71/715966fb0887b0736bf63c8b62fb5bbc.gif) ,
,
 ,
,
(2)  .
.
Levá strana v (2) je tedy komplexní číslo s reálnou částí  a imag. částí
a imag. částí  . Ke splnění (2)
. Ke splnění (2)
je proto nutné a postačuijící, aby  . Dostáváme tak soustavu
. Dostáváme tak soustavu
(3)  .
.
O čísle  předpokládáme v tomto kroku, že je kladné, proto jím můžeme dělit. Z druhé rovnice soustavy (3) tak dostáváme
předpokládáme v tomto kroku, že je kladné, proto jím můžeme dělit. Z druhé rovnice soustavy (3) tak dostáváme  ,
,
odtud (vzhledem k podmínce  )
)  .
.
Tato dílčí řešení nyní postupně dosadíme do první rovnice soustavy (3) . Dostaneme tak
a)  :
:  , takže
, takže  , avšak tato rovnice nemá kladné řešení;
, avšak tato rovnice nemá kladné řešení;
b)  :
:  , takže
, takže  , odtud
, odtud  ;
;
c)  :
:  , takže
, takže  , odtud
, odtud  .
.
ZÁVĚR: Rovnice  má v oboru komplexních šísel tyto kořeny:
má v oboru komplexních šísel tyto kořeny: 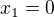 ,
,  ,
, .
.
Offline
