Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 08. 04. 2013 21:31 — Editoval Nikola.brtvova (08. 04. 2013 23:16)
- Nikola.brtvova

- Zelenáč
- Příspěvky: 16
- Reputace: 0
Součet nekonečné řady
Děkuji za vyřešení prvního příkladu, ale ještě těžšíí se mi zdá příklad kdy mám udělat součet řady n(sin  )
)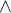 n-1/3
n-1/3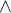 n
n
a další příklad 1/ n* n
n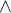 2 +1 vše je pod odmocninou
2 +1 vše je pod odmocninou
a další příklad 1/(2n-1)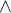 2
2
a další příklad 1/n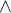 2 - 2n +4
2 - 2n +4
Kdyby bylo možné aspoň k těm příkladům napsat nějaké smysluplné a srozumitelné kroky, které pochopím i já? Máme na dvě věci skripta ve kterých moc postupy pro mě skoro lajka v tomto nejsou. Děkuji za pomoc.
Offline
#3 08. 04. 2013 22:24
Re: Součet nekonečné řady
Součet  je konvergentní, takže součet této řady je také určitě konvergentní. Zatím jsem nikdy podobný příklad nepočítal, ale viděl bych to asi takto:
je konvergentní, takže součet této řady je také určitě konvergentní. Zatím jsem nikdy podobný příklad nepočítal, ale viděl bych to asi takto:
Rozložím na parciální zlomky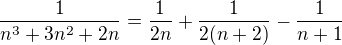
a potom vyčíslím první dva členy prvního zlomku a první člen druhého zlomku, abych dostal stejný jmenovatel a mohl zlomky sečíst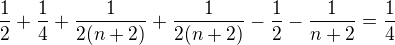 .
.
Když na kalkulačce sečtu prvních pár členů, tak se to 1/4 blíží, tak jsem snad uvažoval správně.
ŘEŠTE FYKOS!
Offline
#5 08. 04. 2013 22:29
- Nikola.brtvova

- Zelenáč
- Příspěvky: 16
- Reputace: 0
Re: Součet nekonečné řady
↑ MirekH: děkuji moc ;) je to správný výsledek já výsledek mám v účebnici, ale nikdo mi nebyl schopen vysvětlit postup, jelikož máme vždy jen geometrické řady a toto není geometrická
Offline
#6 08. 04. 2013 22:35
Re: Součet nekonečné řady
Já to logicky rozkládala na parciální zlomky následovně: A/n + B/(n+1) + C/(n+2) a potom si dopočítala A,B,C atd. Nicméně výsledek mi pak vyšel nula, takže by mě opravdu zajímalo, proč jsi to rozložil tak, jak jsi to rozložil :)
Offline
#7 08. 04. 2013 23:08
Re: Součet nekonečné řady
Zdravím,
pokud by se to mělo vyřešit pořádně, tak to půjde tak, že se nejprve spočítá součet mocninné řady 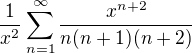 , což lze snadno tak, že se to zderivuje třikrát člen po členu, čímž vznikne obyčejná geometrická řada. Příslušný součet se zpět spočítá trojitým integrováním, vyjde
, což lze snadno tak, že se to zderivuje třikrát člen po členu, čímž vznikne obyčejná geometrická řada. Příslušný součet se zpět spočítá trojitým integrováním, vyjde 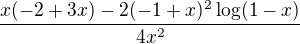 , což v bodě x=1 je jedna čtvrtina a toto číslo je součtem původní řady, protože víme, že byla konvergentní.
, což v bodě x=1 je jedna čtvrtina a toto číslo je součtem původní řady, protože víme, že byla konvergentní.
Offline
