Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#3 15. 04. 2013 13:26
Re: Binomický rozvoj
↑ luuu:
ahoj, já bych se tě prvně zeptal, jestli víš, co je to binomický rozvoj, protože když si jej napíšeš, měl bys už mít vcelku jasno. :)
Což je to možné! Tento stařičký světec ještě ani nezaslechl v svém lese, že bůh je mrtev!
Offline
#4 15. 04. 2013 13:41 — Editoval Honzc (15. 04. 2013 13:48)
Re: Binomický rozvoj
↑ luuu:
Binomický rozvoj 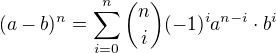
Pro tvůj případ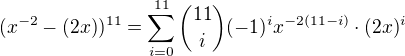
Nejdříve je potřeba ze zadání spočítat 
tedy 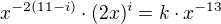
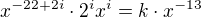


Z toho spočítáš 
Koeficient pak spočítáš z toho vzorečku nahoře a nezapomeň ho ještě vynásobit číslem 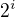
Offline
#6 15. 04. 2013 13:57
Re: Binomický rozvoj
Super! Už v tom začínám mít jasno! Díky za pomoc!
Ještě mám jeden příklad, ale ten se netýká biomického rozvoje...
Kolik je prvků, jestliže počet variací druhé třídy z nich vytvořených bez opakování je o 28 větší než počet kombinací druhé třídy z nich vytvořených bez opakování.
Offline
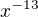 v binomickém rozvoji
v binomickém rozvoji  pro x(nerovná)0 je roven číslu??
pro x(nerovná)0 je roven číslu??
