Matematické Fórum

Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.

Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.

Nejste přihlášen(a). Přihlásit

Stránky: 1

 

#1 15. 04. 2013 14:33 — Editoval found (15. 04. 2013 14:33)

found
Místo: Plzeň
Příspěvky: 392
Škola: TF MFF UK
Pozice: student
Reputace:   22 
Web
 

Ztotožnení komplexních čísel a R^2

Ahoj,

tenhle dotaz je jen takový z jednodušších. Když mám komplexní čísla C a vezmu si libovolné číslo

$ z = a + bi \in \mathbb{C} $

a vytvořím zobrazení 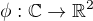$\phi: \mathbb{C} \to\mathbb{R}^2$, které ztotožňuje komplexní čísla a reálnou plochu, potom tvrdím, že ty dva prostory se dají ztotožnit, jelikož $\phi$ je izomorfismus? Nebo musím jít ještě někam dál?

Díky
J.

Což je to možné! Tento stařičký světec ještě ani nezaslechl v svém lese, že bůh je mrtev!

Offline

  • (téma jako vyřešené označil(a) found)

#2 15. 04. 2013 15:21 — Editoval vlado_bb (15. 04. 2013 15:21)

vlado_bb
Moderátor
Příspěvky: 6255
Škola:
Reputace:   145 
 

Re: Ztotožnení komplexních čísel a R^2

↑ found:Ako mnoziny ano, pretoze uvedene zobrazenie je bijekcia. Ale to, co robi komplexne cisla komplexnymi cislami a realnu plochu realnou plochou, su prace operacie. A tie sa uz podstatnym sposobom lisia.

Offline

 

#3 15. 04. 2013 18:19

martisek
Příspěvky: 914
Škola: MU Brno
Pozice: učitel, FSI VUT v Brně
Reputace:   52 
 

Re: Ztotožnení komplexních čísel a R^2

↑ vlado_bb:  ↑ found:

Téma je sice vyřešené, ale úplně špatně....

Wolfram ani jiný chemický prvek matematiku nenaučí.

Offline

 

 

Stránky: 1

Zápatí

Powered by PunBB
© Copyright 2002–2005 Rickard Andersson