Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 15. 04. 2013 21:38 — Editoval Miky4 (15. 04. 2013 21:46)
Re: Rovnice s Odmocninami
↑ filipi123:
Ahoj, umocníš, na levé straně necháš jen odmocninu a znova umocníš co ti vyjde upravíš na součin a provedeš zkoužku, kterou eliminuješ jeden ze dvou kořenů vzniknuvší rovnice a získáš jen jeden kořen rovnice původní..
Offline
#3 15. 04. 2013 21:49
Re: Rovnice s Odmocninami
↑ Miky4:
Ahoj, díky za odpověd, to ještě vím mám umocnit, ale nepamatuji si přesně jak to funguje, když umocním zmizí my odmocnina na levé straně, co se děje na pravé?, když odmocním po druhé co se děje na levé straně s tím 4x na druhou, odmocněním z něho vznikne 4x na třetí nebo 16x, nebo se sním neděje nic ? děkuji velice
Offline
#4 15. 04. 2013 21:56 — Editoval Miky4 (15. 04. 2013 21:56)
Re: Rovnice s Odmocninami
filipi123 napsal(a):
co se děje na pravé?
Aplikuješ vzorec 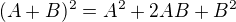
filipi123 napsal(a):
co se děje na levé straně s tím 4x na druhou
Člen 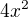 ti zmizí jelikož ho máš na obou stranách a odečteš ho tedy.
ti zmizí jelikož ho máš na obou stranách a odečteš ho tedy.
filipi123 napsal(a):
odmocněním z něho vznikne 4x na třetí nebo 16x
Nicméně jeho umocněním by vzniklo 
Offline
#5 15. 04. 2013 22:06 — Editoval bejf (15. 04. 2013 22:29)
Re: Rovnice s Odmocninami
↑ filipi123:
Ahoj.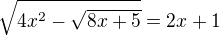 umocníš na druhou
umocníš na druhou
 tady sečteme a tím nám zmizí
tady sečteme a tím nám zmizí 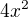
 znovu umocníš
znovu umocníš posčítáme
posčítáme

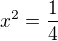 odmocníš
odmocníš
Jelikož umocňování není ekvivalentní úprava, musíš udělat zkoušku. Dosadíš nejdřív  a pak
a pak 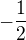 do původní rovnice.
do původní rovnice.
Offline
#6 15. 04. 2013 22:08 Příspěvek uživatele filipi123 byl skryt uživatelem filipi123.
#8 15. 04. 2013 22:20
Re: Rovnice s Odmocninami
↑ bejf:
Moc díky za pomoc oboum dostal jsem se k 5 řádku pak jsem nevěděl co stím, jak se zbavit toho x na druhou, ted už to chápu, ale ještě jeden dotaz tento příklad dělám jako opravu čtvrletky a mám tam od učitele napsaný jen správný výsledek x= -0,5 (jedna polovina=>Lse nesmí rovnat P) jaktože výjde -0.5 když odmocnina z jedné čtvrtiny je 0,5 ?
Offline
#9 15. 04. 2013 22:24 — Editoval Miky4 (15. 04. 2013 22:30)
Re: Rovnice s Odmocninami
↑ filipi123:
Proč jeden výsledek, to jsme ti už oba napsali. Na tu otázku na konci ti odpovím tak, že tě bejf zbytečně mate postupem, který se neučí, a ve kterém by správně mělo být pár kroků navíc.
Offline
#10 15. 04. 2013 22:25 Příspěvek uživatele filipi123 byl skryt uživatelem filipi123.
#13 15. 04. 2013 22:37 — Editoval Miky4 (15. 04. 2013 22:40)
Re: Rovnice s Odmocninami
↑ filipi123:
Rovnice v součinovém tvaru jste se už museli učit. Kořeny získáš vypočítáním, kdy se ty zavorky rovnají nule. Máš dva adepty na kořen. Oba dosadíš do zadání rovnice a pro 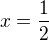 ti vyjde to, co ti napsal učitel, totiž
ti vyjde to, co ti napsal učitel, totiž 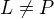 .
.
Offline
#14 15. 04. 2013 22:38
Re: Rovnice s Odmocninami
↑ filipi123:
Vyjdou ti kořeny dva. Jeden je 0,5 a druhý -0,5. Díky umocnění ti ale může vzniknout falešný kořen, takže musíš udělat zkoušku.
Pokud nějaký z těch kořenů po dosazení do původní rovnice splňuje zadanou rovnost, tak je kořenem té původní rovnice. Pokud nesplňuje rovnost, odhalil jsi falešný kořen, který musíš vyřadit z tvé odpovědi.
Offline
#16 17. 04. 2013 19:31
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Rovnice s Odmocninami
↑ filipi123:
pokud sleduji celý vývoj tématu, tak dotaz je zkoušku pro iracionální rovnici z úvodního příspěvku. Zkoušku vždy provádíme dosazováním do původního zadání rovnice. A to proto, že úpravy mohou být chybné nebo neekvivalentní (potom by zkouška neměla smysl).
Lze označit za vyřešené? Děkuji.
Offline
#19 21. 04. 2013 09:10
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Rovnice s Odmocninami
Zdravím.
↑ filipi123:
děkuji, v pravém dolním rohu 1. příspěvku je tlačítko pro označení.
↑ dorfik:
to asi není původní rovnice z 1. příspěvku ↑ filipi123:? Děkuji.
Offline
#21 21. 04. 2013 11:35
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Rovnice s Odmocninami
↑ dorfik:
a tak - děkuji. To se asi nedá. Pokud jsi představil, že jsi pravou stranu umocnil a tak poslal pod odmocninu nalevo, tak ani to umocnění není v pořádku. A nemůžeme poslat pod odmocninu člen, který není v násobku (ale v součtu nebo rozdílu).
Např. výraz  už nevylepšíme posláním 1 pod odmocninu. Souhlasíš? Řekla bych, že u Tebe v návrhu jen nepozornost v úpravě - je tak? Děkuji.
už nevylepšíme posláním 1 pod odmocninu. Souhlasíš? Řekla bych, že u Tebe v návrhu jen nepozornost v úpravě - je tak? Děkuji.
Offline


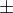 tak ano. Nás to učili takhle
tak ano. Nás to učili takhle  =>
=> 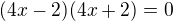 . Zkoušku musíme dělat z jiného důvodu, totiž kvůli umocnění.
. Zkoušku musíme dělat z jiného důvodu, totiž kvůli umocnění.


