Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 30. 04. 2013 12:35 — Editoval dorfik (30. 04. 2013 13:01)
Vektory
Úloha zní : Která z uvedených přímek .... je kolma k přímce p.
Z grafu jde vidět, že má přímka p body v bodech ![kopírovat do textarea $A[3,2]$](/mathtex/bb/bb04ca9abb92c6ee896e18d4481af485.gif) a
a ![kopírovat do textarea $B[-3,-2]$](/mathtex/db/dbf0e9853ef688419a2fadcfa89713cf.gif)
Nenapadá mě nic jinýho, než udělat si rovnici osy úsečky.
Vyjde mi 
Výsledkem úlohy je přímka : 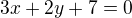
tak se chci zeptat, jestli záleží na hodnotě C ?, které se dopočítát nemůžu.
jestli je rozhodující pouze  a za C si mohu dosadit cokoli
a za C si mohu dosadit cokoli
Offline
- (téma jako vyřešené označil(a) dorfik)
#6 30. 04. 2013 12:43
- 010010

- Příspěvky: 82
Re: Vektory
nájdi smerový vektor každej priamky, a porovnaj ich skalárnym súčinom.
Hodnotu C dopočítaš tak, že za x,y dosadíš nejaký bod, ktorý leží na danej priamke tak, aby rovnica platila.
Offline
#11 30. 04. 2013 13:11
Offline
#12 30. 04. 2013 13:26 — Editoval Cheop (30. 04. 2013 13:38)
- Cheop


- Místo: okres Svitavy
- Příspěvky: 8209
- Škola: PEF VŠZ Brno (1979)
- Pozice: důchodce
- Reputace: 366
Re: Vektory
↑ dorfik:
Tak ten př. 20
Přímka p prochází body: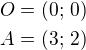
Její směrový vektor je: 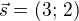 = normálový vektor kolmé přímky
= normálový vektor kolmé přímky
Rovnice kolmice bude : no a jediná přímka , která má u x 3 a zároveň u y +2 je z nabízených možností přímka:
no a jediná přímka , která má u x 3 a zároveň u y +2 je z nabízených možností přímka: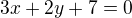
odpověď E
Nikdo není dokonalý
Offline
 tj: např.
tj: např. atd.
atd.![kopírovat do textarea $A[3;2] ; B[-3;-2]$](/mathtex/24/24c6af580f07c0faa24329cae8772681.gif)
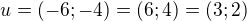 = normalovej vektor kolmé přímky
= normalovej vektor kolmé přímky