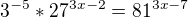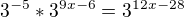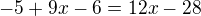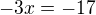Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 01. 05. 2013 14:18 — Editoval wolfito (01. 05. 2013 14:54)
Exponencialní rovnice
Zdravíčko,
potřeboval bych něco trochu vysvětlit.
Mam tu lehkou exponencialní rovnici: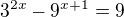
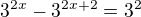 -ted to mužu přepsat na:
-ted to mužu přepsat na: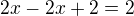 - jde mi o to jestli tam kde je to minus ma byt plus. Kdyz se v exponencialni rovnici odečíta.
- jde mi o to jestli tam kde je to minus ma byt plus. Kdyz se v exponencialni rovnici odečíta.
Radost z uvažování a z chápání je nejkrásnějším darem přírody.
Offline
- (téma jako vyřešené označil(a) wolfito)
#2 01. 05. 2013 14:55 — Editoval nejsem_tonda (01. 05. 2013 14:55)
- nejsem_tonda

- Příspěvky: 649
- Reputace: 54
Re: Exponencialní rovnice
Zdravim,
jaka uvaha vede k tomu, ze se budeme divat jen na exponenty?
Plati neco jako 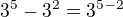 ?
?
Offline
#3 01. 05. 2013 15:01
Re: Exponencialní rovnice
↑ nejsem_tonda:
Pokud v exponencialni rovnici mame stejny zaklady tak potom mužeme zaklady vypustit a počítame jen s exponentama. 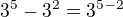 - tohle jsem netvrdil že něco takovyho platí.
- tohle jsem netvrdil že něco takovyho platí.
Radost z uvažování a z chápání je nejkrásnějším darem přírody.
Offline
#4 01. 05. 2013 15:02
Re: Exponencialní rovnice
↑ wolfito:
Ale tvrdil, resp. tvrdíš, že 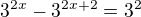
Příspěvky psané červenou barvou jsou moderátorské, šedá je offtopic.
Offline
#6 01. 05. 2013 15:11
Re: Exponencialní rovnice
↑ wolfito:
Ano, samozřejmě, zapomněl jsem ke svému příspěvku něco připsat, tedy:
ty tvrdíš, že z 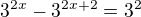 plyne
plyne 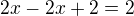 , což není pravda, zkus to nějak opravit.
, což není pravda, zkus to nějak opravit.
Příspěvky psané červenou barvou jsou moderátorské, šedá je offtopic.
Offline
#7 01. 05. 2013 15:11
Re: Exponencialní rovnice
↑ wolfito:
To ano, ale už nemůžeš udělat ten další krok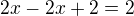 toto už je špatně.
toto už je špatně.
Postup: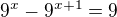
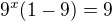
atd
Pořádek je pro blbce, inteligent zvládá chaos!
Offline
#9 01. 05. 2013 15:13
- nejsem_tonda

- Příspěvky: 649
- Reputace: 54
Re: Exponencialní rovnice
↑ wolfito:
Jasne, rozumim tve uvaze. Tva uvaha vychazi z pravidla, ktere ti nekdo poskytl.
Pojdme vyresit jeste jednodussi rovnici: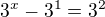
Podle drivejsiho postupu bychom mohli misto toho resit rovnici: ,
,
takze mame reseni x=3. Zkus dosadit.
Offline
#10 01. 05. 2013 15:14
Re: Exponencialní rovnice
↑ zdenek1:
Jaktože to tak nemužu udělat? Když mam společny zaklad tak mužu pracovat jen s exponenty ne? Dělal jsem takhle x příkladu a vždycky mě vyšel spravný vysledek.
Radost z uvažování a z chápání je nejkrásnějším darem přírody.
Offline
#12 01. 05. 2013 15:34
- nejsem_tonda

- Příspěvky: 649
- Reputace: 54
Re: Exponencialní rovnice
Nezbyva nez si rozmyslet, zda a kdyztak proc plati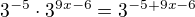
(samozrejme je snazsi rozmyslet si to na necem jednodussim, napr. 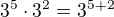 )
)
Offline
#14 01. 05. 2013 15:42
- nejsem_tonda

- Příspěvky: 649
- Reputace: 54
Re: Exponencialní rovnice
↑ wolfito:
Skvely zaver!
Pro me by mozna jeste zajimavejsi zaver byl nedivat se na ulohy jako na chvilky stravene pouzivanim pravidel, ktere mi nekdo shora prinesl.
Offline
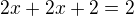 takhle?
takhle?