Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Střední škola
- » Slovní úlohy řešené pomocí derivací (TOTO TÉMA JE VYŘEŠENÉ)
#1 01. 05. 2013 01:08
Slovní úlohy řešené pomocí derivací
Ahoj:), rád bych se Vás zeptal, jak by se řešila tato úloha? Řešil jsem totožnou úlohu akorát nádoba byla s víkem. Nějak tomu nerozumím, děkuji
Zadání:
66) Určete rozměry válcové nádoby bez víka tak aby při objeme 2 litry měla nádoba minimální povrch.
Offline
- (téma jako vyřešené označil(a) bonifax)
#2 01. 05. 2013 02:31 — Editoval 010010 (01. 05. 2013 02:41)
- 010010

- Příspěvky: 82
Re: Slovní úlohy řešené pomocí derivací
objem valca: 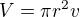
povrch valca: (nebudeme potrebovať)
(nebudeme potrebovať)
povrch valca bez veka(bez jednej podstavy): 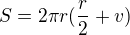 V tomto vzorci sme "stratili" veko.
V tomto vzorci sme "stratili" veko.
Vieme: 
chceme zistiť minimálny povrch, tak dosadíme do vzorca na výpočet povrchu, teda: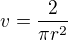 do
do 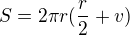 máme
máme 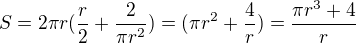
Prvá derivácia podľa premennej r sa rovná: 
Určíme stacionárne body(body, v ktorých sa prvá derivácia rovná nule).
Vidíme že jeden bod je  ale to nieje naše hľadané číslo, pretože táto hodnota nemá zmysel.
ale to nieje naše hľadané číslo, pretože táto hodnota nemá zmysel.
Druhý bod zistíme 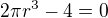 teda
teda ![kopírovat do textarea $r=\sqrt[3]{\frac{2}{\pi }}$](/mathtex/7a/7aa9c38d55194b2153b0c4f53fa4a01e.gif) , ľahko sa overí, že tento bod je lokálne minimum.
, ľahko sa overí, že tento bod je lokálne minimum.
Takže poznáme polomer. Dosadíme ho do pôvodnej rovnice, pre výpočet objemu, a dopočítame výšku nášho valca. Teda: ![kopírovat do textarea $v=\frac{2}{\sqrt[3]{4\pi }}$](/mathtex/0e/0e84a892131c10674b0d6e89835a039c.gif)
Offline
#3 01. 05. 2013 16:12
Re: Slovní úlohy řešené pomocí derivací
Ahoj, velmi hezké, děkuji moc:) ještě bych se rád zeptal na malý detail.
Týká se to dopočítání výšky. Na kalkulačce to vychází dobře. Jen nechápu přesnou úpravu do té podoby, kterou jsi uvedl.
![kopírovat do textarea $=\frac{2}{\sqrt[3]{4\pi }}$](/mathtex/64/642e9ba41115e7ec3068bf80fd7c0fe5.gif)
Offline
Stránky: 1
- Hlavní strana
- » Střední škola
- » Slovní úlohy řešené pomocí derivací (TOTO TÉMA JE VYŘEŠENÉ)
![kopírovat do textarea $\frac{2}{\pi (\sqrt[3]{\frac{2}{\pi }})^2}=\frac{2}{\pi \sqrt[3]{\frac{4}{\pi ^2}}}=\frac{2}{\sqrt[3]{\frac{4\pi ^3}{\pi ^2}}}$](/mathtex/8a/8ad71cf926673312fbe791c67e9dc69c.gif)
![kopírovat do textarea $\sqrt[3]{\pi ^3}=\pi $](/mathtex/ab/ab6504193b7b8713af106e56537af214.gif) a
a ![kopírovat do textarea $\sqrt[n]{x}*\sqrt[n]{y}=\sqrt[n]{xy}$](/mathtex/9b/9b2e79a971c82432b47a705556feb3a4.gif)