Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 28. 10. 2012 15:19
- check_drummer

- Příspěvky: 4637
- Reputace: 99
Algebraicky uzavřená tělesa obsahující Q
Ahoj,
najděte algebraicky uzavřená tělesa (izomorfní považujte za totožná), která obsahují Q (racionální čísla).
Je zřejmé, že takovým tělesem je C (komplexní čísla) a také T:=Q(A), kde A jsou všechna algebraická čísla, tj. A jsou kořeny všech polynomů s racionálními koeficienty. Tedy Q(A) je těleso generované Q a A. Je také zřejmé, že "mezi" Q a T již žádné takové těleso neexistuje. Tedy otázka je, zda existují algebraicky uzavřená tělesa mezi T a C a nebo algebraicky uzavřené těleso obsahující C.
"Máte úhel beta." "No to nemám."
Offline
#2 30. 10. 2012 19:14
- check_drummer

- Příspěvky: 4637
- Reputace: 99
Re: Algebraicky uzavřená tělesa obsahující Q
↑ check_drummer:
Napadlo mě, že bychom mohli uvažovat libovolný transcendentní prvek nad Q, např. e a uvažovat T1 algebraický uzávěr tělesa T(e). Pokud není T(e)=C, pak bychom mohli opět uvažovat nějaký transcendentní prvek f nad T1 a uvažovat T2 algebraický uzávěr tělesa T1(e). Otázka pak je, zda bude tato posloupnost těles Ti (alg. uzávěrů) konečná nebo nekonečná. Řekl bych, že konečná nespočetná.
"Máte úhel beta." "No to nemám."
Offline
#3 01. 05. 2013 20:59 — Editoval OiBobik (01. 05. 2013 23:18)
- OiBobik

- Moderátor

- Místo: Brno/Praha
- Příspěvky: 1013
- Škola: MFF UK Mat. struktury
- Pozice: student
- Reputace: 82
Re: Algebraicky uzavřená tělesa obsahující Q
↑ check_drummer:
Ahoj,
v dlouhé chvíli jsem tu šmejdil po fóru a narazil na toto téma.
Pokud si to pamatuju správně, tak pro  nekonečné těleso a
nekonečné těleso a 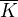 jeho algebraický uzávěr platí, že
jeho algebraický uzávěr platí, že 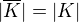 .
.
Takže konstrukce tak, jak ji navrhuješ (povedeš-li ji transfinitní indukcí, tj budeš číslovat ordinály; "limitní" těleso by asi mohl být alg. uzávěr sjednocení všech předchozích těles, což by mělo být těleso), by měla skutečně vyprodukovat nespočetný řetězec alg. uzavřených těles mezi  a
a  .
.
Co se týče té druhé části: Tam by to mělo jít také hladce, stačí jako transcendentní prvek přidávat vždy novou neurčitou (takže ta posloupnost by vypadala:  ).
).
Jo a ještě poznámka (k názvu): Kdykoli má člověk těleso charakteristiky 0, pak to těleso obsahuje jako prvotěleso Q (nebo isomorfní těleso). Takže "Algebraicky uzavřená těleso obsahující Q" je, technicky vzato, libovolné alg. uz. těleso charakteristiky 0.
Jo a ještě jedna poznámka: Aby ty argumenty výše fungovaly, je ještě potřeba nahlédnout, že 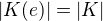 pro každé nekonečné těleso
pro každé nekonečné těleso  a každý prvek
a každý prvek  z nějakého rozšíření (tj. i když je
z nějakého rozšíření (tj. i když je  nad
nad  transcendentní).
transcendentní).
"The first rule of Tautology Club is the first rule of Tautology Club." [xkcd]
Offline