Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 02. 05. 2013 17:36 — Editoval MirekH (02. 05. 2013 20:14)
Řešení maturity jaro 2013 s postupy (neoficiální)
Kdyby byl nějaký postup moc stručný, dejte vědět a já ho rozepíšu detailněji.
Pokud najdete nějaké překlepy, budu rád, když mě na ně upozorníte.
Pokud si chcete ověřit postupy i z jiného zdroje, můžete se podívat zde na řešení na webu Nabla (autorem je Michal Staruch).
1) [1 b]
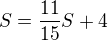
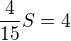

2) [1 b]
Rovnou kalkulačka: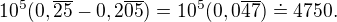
Zlomky: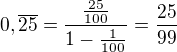
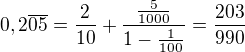
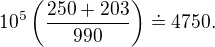
3) [1 b]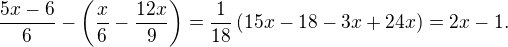
4) [max. 3 b]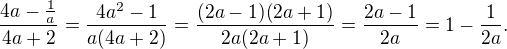
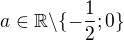
5) [max. 2 b]



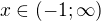
6) [1 b]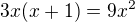
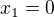 ... můžu dělit
... můžu dělit 
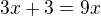
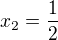
7) [1 b]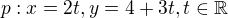
Přes normálový vektor: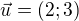 ... koeficienty u parametrů
... koeficienty u parametrů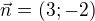 ... prohodíme souřadnice a u jedné změníme znaménko
... prohodíme souřadnice a u jedné změníme znaménko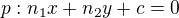
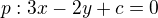
Dosadíme 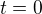 a dostaneme bod přímky
a dostaneme bod přímky ![kopírovat do textarea $[0;4]$](/mathtex/bb/bbd5056ba3a95cc7ac9d83a8d3937c8f.gif) , dosadíme do obecné rovnice:
, dosadíme do obecné rovnice: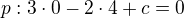

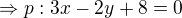
Přes směrnicový tvar:
Lineární člen  určíme z bodu
určíme z bodu ![kopírovat do textarea $[0;4]$](/mathtex/bb/bbd5056ba3a95cc7ac9d83a8d3937c8f.gif) , takže
, takže  . Směrnicový tvar
. Směrnicový tvar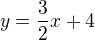
ekvivalentními úpravami předěláme na tvar obecný.
Jako soustavu rovnic: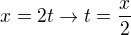 ,
,
dosadíme do vztahu pro y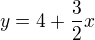
a opět vše převedeme na levou stranu.
8) [max. 2b]![kopírovat do textarea $A[-2;-1], C[-1;3], \vec{CB} = (2; -3)$](/mathtex/db/dbd51b3b661a256e0bf60561ec6884df.gif)
Souřadnice bodu B získáme přičtením vektoru k souřadnicím bodu C: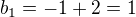
![kopírovat do textarea $b_2 = 3 - 3 = 0 \Rightarrow B[1;0]$](/mathtex/a2/a24ff219235506d72dd70ef0a4b852c8.gif)
Pro souřadnice středu S strany AC platí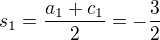
![kopírovat do textarea $s_2 = \frac{a_2 + c_2}{2} = 1 \Rightarrow S[-\frac{3}{2};1]$](/mathtex/a8/a87bea68c4d3baf2c94718da6f880cca.gif)
9) [max. 2 b]
Medián je hodnota uprostřed uspořádaného souboru, přesněji pro lichý počet prvků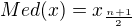
a pro sudý počet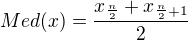 .
.
Sečtením výšek sloupců zjistíme, že soubor má 25 prvků, medián je tedy hodnota třináctého členu, což je 1.
Aritmetický průměr: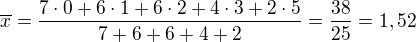
10) [1 b]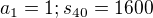
Obecně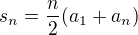 ,
,
pro nás tedy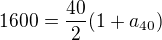

11) [1 b]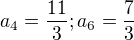
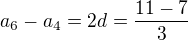
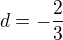

12) [max. 2 b]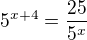
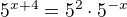
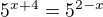
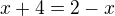

13) [max. 2 b]
Výkon linky je  ,
, ![kopírovat do textarea $[V] = \mathrm{den}^{-1}$](/mathtex/f7/f744f260dd8ef9067d1f0e1c97a3c049.gif) .
.
Pracuje 2 dny na 25%, 2 dny na 50%, den na 100%, celkem vyrobí 720.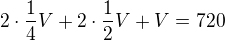
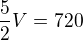
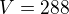
Za pět dní při plném výkonu tedy vyrobí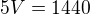
14) [max. 3 b] ... chlapci,
... chlapci,  ... dívky,
... dívky,  ... družstvo
... družstvo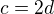
Chlapcům do družstva 12 přebývá, dívkám 1 chybí. Soustava
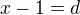
Druhou rovnici vynásobíme -1 a sečteme s první, dostaneme přímo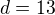
V oddílu je tedy celkem 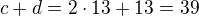 členů.
členů.
15) [max. 2 b]
V pravoúhlém trojúhelníku RPX určíme pomocí Pyth. v.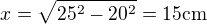
V pravoúhlém RPQ opět P. v.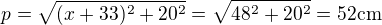
16) [max. 2 b]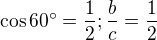 ... ANO (je pravoúhlý)
... ANO (je pravoúhlý)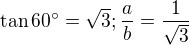 ... NE
... NE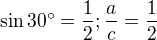 ... ANO
... ANO ... ANO
... ANO
17) [2 b] C
První troj. je tupoúhlý rovnoramenný, ortocentrum tedy leží vně (tzn. mimo obrazec).
Druhý troj. je ostroúhlý rovnoramenný, průsečík výšek leží uvnitř.
Třetí troj. je pravoúhlý, ortocentrum splývá s bodem u pravého úhlu a není tedy vně.
Čtvrtý troj. je opět tupoúhlý rovnoramenný.
... celkem 2 troj.
18) [2 b] E
Vrcholové úhly jsou shodné, tudíž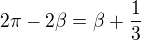
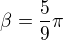
19) [2 b] D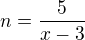
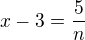
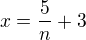
20) [2 b] B
Ve válci platí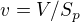 ,
,
kde 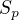 je obsah podstavy. Dosazením
je obsah podstavy. Dosazením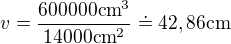
Voda dosahuje pouze 3/4 výšky, takže
21) [2 b] A
Protáhneme-li rovné části obalu, dostaneme rovnoramenný trojúhelník. Spustíme-li ze středu jedné z kružnic kolmice na obal, vytvoří paty kolmic, vrchol velkého trojúhelníku a střed kružnice deltoid s úhly 90°, 90°, 60° a  . Součet úhlů čtyřúhelníku je 360°, takže
. Součet úhlů čtyřúhelníku je 360°, takže 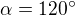 . Kružnice jsou celkem tři, takže trojnásobným započítáním oblouku se středovým úhlem
. Kružnice jsou celkem tři, takže trojnásobným započítáním oblouku se středovým úhlem  dostaneme celou kružnici. Každá z rovných částí obalu má délku
dostaneme celou kružnici. Každá z rovných částí obalu má délku 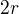 (po zmíněném zakreslení kolmic by to mělo být zjevné z obdélníků, které v náčrtku vzniknou). Celkový obsah obalu je obvod krát výška, takže
(po zmíněném zakreslení kolmic by to mělo být zjevné z obdélníků, které v náčrtku vzniknou). Celkový obsah obalu je obvod krát výška, takže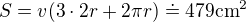
22) [2 b] B
Kód má celkem pět míst, z toho první a poslední je pevně dané - zajímají nás tedy pouze 3 místa. Dále je dáno, že číslice musí být různé - po použití číslic 8 a 5 jich zbývá už pouze osm. Jedná se tedy o variaci bez opakování třetí třídy z osmi prvků: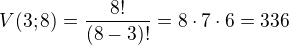
23) [2 b] C
Z 25 žáku je 10 připravených, učitel losuje 5. Ptají se nás na prvního vylosovaného žáka, údaj o celkovém počtu losovaných je tudíž nepodstatný. Pravděpodobnost, že bude první žák připraven, že počet připravených ku celkovému počtu, tedy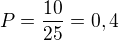
24) [2 b] E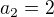
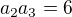
Třetí člen zapíšeme jako  , takže
, takže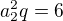
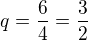 .
.
Vylučovací metodou: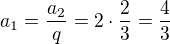 ... správně
... správně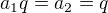 ... správně
... správně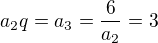 ... správně
... správně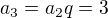 ... správně
... správně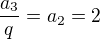 ... v zadání je
... v zadání je  , takže špatně
, takže špatně
25) [max. 4 b] B, F, D, A
Tohle je myslím zjevné, jen pro pořádek: koeficient lineárního členu určuje sklon (tangens, derivace), absolutní člen určuje posun po ose y - stačí tedy odečíst z grafu hodnotu funkce v x=0.
26) [max. 3 b] A, C, D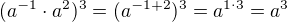

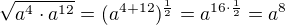
ŘEŠTE FYKOS!
Offline
#2 02. 05. 2013 17:59
- Hawkey1234

- Zelenáč
- Příspěvky: 15
- Reputace: 0
Re: Řešení maturity jaro 2013 s postupy (neoficiální)
U 26.2. správný postup, ale místo B, má být C..jinak krása, dostáváš zlatýho bludišťáka :)
Offline
#3 02. 05. 2013 18:02 — Editoval MirekH (02. 05. 2013 18:03)
Re: Řešení maturity jaro 2013 s postupy (neoficiální)
↑ Hawkey1234:
Díky, opraveno.
Btw, u psaní úvodního příspěvku jsem pochopil, proč bylo na test 90 minut: Zadavatelé mysleli, že to studenti budou psát v TeXu.
ŘEŠTE FYKOS!
Offline
#4 02. 05. 2013 18:13
- Hawkey1234

- Zelenáč
- Příspěvky: 15
- Reputace: 0
Re: Řešení maturity jaro 2013 s postupy (neoficiální)
Ber v úvahu to, že maturitu skládají i slabší žáci a pro ně je i těch 90 minut málo..no a o stresu ani nemluvím :)
Offline
#5 02. 05. 2013 18:14
Re: Řešení maturity jaro 2013 s postupy (neoficiální)
Zdravím,
měl bych dotaz. Vím, že maturity neopravujete, ale u příkladu číslo 5 jsem uvedl jen že x > -1 ,ale na množinu jsem zapomněl. Myslíte si, že mi uznají za 2 body či jen za 1 bod?
Offline
#6 02. 05. 2013 18:21 — Editoval bejf (02. 05. 2013 18:22)
Re: Řešení maturity jaro 2013 s postupy (neoficiální)
↑ tommmic:
Měla by být uznána i ta podmínka, která říká naprosto to samé. Zadání neříká, aby výsledek byl zapsán intervalem.
Offline
#7 02. 05. 2013 18:22
Re: Řešení maturity jaro 2013 s postupy (neoficiální)
↑ tommmic:
V zadání není výslovně uvedeno, že by řešení mělo být vyjádřeno pomocí intervalu. Odpověď x > -1 je tedy dle mého názoru postačující, nicméně za Cermat neručím.
ŘEŠTE FYKOS!
Offline
#9 02. 05. 2013 18:27
- Cheop


- Místo: okres Svitavy
- Příspěvky: 8209
- Škola: PEF VŠZ Brno (1979)
- Pozice: důchodce
- Reputace: 366
Re: Řešení maturity jaro 2013 s postupy (neoficiální)
↑ tommmic:
No pokud bych hodnotil já (jakože nehodnotím) dal bych plný počet bodů.
Podle mne je: stejné jako
stejné jako 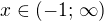
Nikdo není dokonalý
Offline
#10 02. 05. 2013 18:30
Re: Řešení maturity jaro 2013 s postupy (neoficiální)
↑ ibby7321:
Bodovaní máš v zadaní na www.novamaturita.cz
Radost z uvažování a z chápání je nejkrásnějším darem přírody.
Offline
#11 02. 05. 2013 18:32
#14 02. 05. 2013 18:46
Re: Řešení maturity jaro 2013 s postupy (neoficiální)
↑ azas605:
Jde o to, zda se hodnota goniometrické funkce shoduje s poměrem stran, který by měla vyjadřovat. Tangens je protilehlá strana ku přilehlé, takže 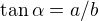 . V části 4 tangens 30° skutečně odpovídá poměru stran, ale v části 2 se jedná o tangens 60° a tyto dvě hodnoty jsou pochopitelně různé.
. V části 4 tangens 30° skutečně odpovídá poměru stran, ale v části 2 se jedná o tangens 60° a tyto dvě hodnoty jsou pochopitelně různé.
ŘEŠTE FYKOS!
Offline
#15 02. 05. 2013 19:01
Re: Řešení maturity jaro 2013 s postupy (neoficiální)
↑ JanS1:
V pátém příkladě se mi při přepisování jaksi ztratil jmenovatel (opraveno). Nicméně se nedomnívám, že by se mohlo jednat o smíšené číslo - to by myslím nemělo obsahovat proměnné, tj. mělo by jít přímo o konkrétní číslo, ne algebraický výraz.
ŘEŠTE FYKOS!
Offline
#19 02. 05. 2013 19:24
Re: Řešení maturity jaro 2013 s postupy (neoficiální)
Dobrý den, také si dovolím přispět s trochou do mlýna.
http://www.nabla.cz/obsah/matematika/st … t-2013.php
Fyzika a matematika konečně srozumitelně - www.nabla.cz
Fyzikální bludy
Řešení státní maturity z matematiky
Kdy psát mě a mně
Offline
#20 02. 05. 2013 19:32
Re: Řešení maturity jaro 2013 s postupy (neoficiální)
↑ kadedemon:
Nejdříve se zbavíme závorek: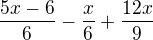
Potom převedeme na společný jmenovatel 18. Čitatele prvních dvou zlomků tedy budeme násobit třemi a čitatele posledního zlomku dvěma: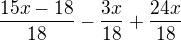
Nyní můžeme vše zapsat jako jeden zlomek: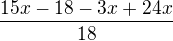
Členy s proměnnou x v čitateli sečteme: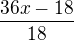
Oba členy v čitateli jsou dělitelné beze zbytku jmenovatelem, výraz můžeme upravit do finálního tvaru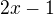 .
.
ŘEŠTE FYKOS!
Offline
#22 02. 05. 2013 19:38
- biologista
- Zelenáč
- Příspěvky: 1
- Pozice: student
- Reputace: 0
Re: Řešení maturity jaro 2013 s postupy (neoficiální)
Dobrý den, mohu vznést dotaz?
V tom čtvrtém příkladu jsem nedošla s úpravami tak daleko - došlo jsem do té předposlední úravy - s tím zlomkem. Myslíte, že to je chyba? A ještě jeden dotaz, ve škole jsme zvyklí psát podmínky řešitelnosti jako x se nesmí rovnat nějakému číslu a ne x leží v R a odečteme od něj interval, ve kterém ležet nemá. A poslední dotaz, zapomněla jsem do podmínek řešitelosti uvést tu nulu. Když za celý tento příklad jsou 3 body, myslíte, že mám šanci alespoň na 2? Budu mít totiž pravděpodobně na rozmezí známku a ráda bych tu lepší. :D
Offline
#23 02. 05. 2013 19:41
Re: Řešení maturity jaro 2013 s postupy (neoficiální)
tu obecnou rovnici jsem neřešil přes normálový tvar nebo tangens. Ale přímo z toho zadání.
x=2t => t=x/2
y=4+(3/2)x => (3/2)x-y+4=0
Je to dobře a nebo jsem náhodou narazil na příklad kde to jenom náhodou vyšlo správně?
Offline
#25 02. 05. 2013 19:45
Re: Řešení maturity jaro 2013 s postupy (neoficiální)
↑ biologista:
Dobrý den,
poslední úprava pravděpodobně hodnocena nebude, zápis ve tvaru 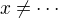 by měl v pořádku. Opomenutí nuly v podmínkách řešitelnosti už je ovšem chyba, takže bych počítal spíše s 2 body.
by měl v pořádku. Opomenutí nuly v podmínkách řešitelnosti už je ovšem chyba, takže bych počítal spíše s 2 body.
ŘEŠTE FYKOS!
Offline
 ale jednou je to není pravouhlý trojuhelník a podruhé je co je správně?
ale jednou je to není pravouhlý trojuhelník a podruhé je co je správně?