Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 01. 05. 2013 15:52 — Editoval Katsushiro (01. 05. 2013 15:58)
- Katsushiro

- Místo: Rožnov pod Radhoštěm
- Příspěvky: 144
- Škola: VŠB TUO - FEI
- Pozice: student
- Reputace: 2
Průběh funkce - kontrola
Jak vidím, kolegyně pode mnou už měla stejný dotaz, jen jiný příklad - pro přehlednost vytvářím nové téma.
Takže, mám rozebrat fci 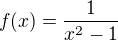
1) Definiční obor
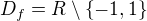
2) Spojitost
Fce je spojitá na intervalech  ,
,  ,
, 
3) Periodicita, sudost/lichost
Fce není periodická.
=> Fce je sudá. - Tady si nejsem jistý, učili jsme se něco ve smyslu, že pokud je fce sudá/lichá, prostě souměrná, stačí určovat jen jednu polovinu (tj. u mě kladnou část Df). Je to možné nebo je to úplná blbina? :D
- Tady si nejsem jistý, učili jsme se něco ve smyslu, že pokud je fce sudá/lichá, prostě souměrná, stačí určovat jen jednu polovinu (tj. u mě kladnou část Df). Je to možné nebo je to úplná blbina? :D
4) 1. derivace, stacionární body, intervaly monotonie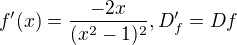

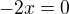
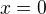
Dále tedy počítám jen s onou polovinou Df:
Pro intervaly  i
i 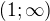 je fce klesající, v 1 je bod nespojitosti.
je fce klesající, v 1 je bod nespojitosti.
5) Druhá derivace, konvexnost/konkávnost

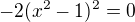
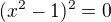

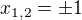
Opět řeším jen na pravé polovině Df:
Na intervalech 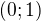 i
i  je fce konkávní.
je fce konkávní.
6) Lokální extrémy
Význačné body: 0;1
Fce nemá lokální extrémy.
7) Limity
body nespojitosti: -1;1
krajní hodnoty Df: -inf; +inf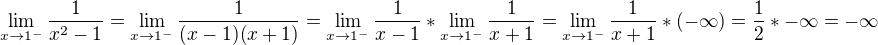
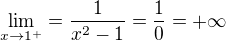

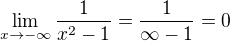
8) Asymptoty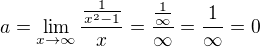
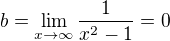
9) Významné body
Vyznamné body máme -1;0;1, jen 0 patří do Df.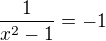
Tady mi lehce není jasné, co se to vlastně uvádí, myslí se tím průsečíky?
10) Náčrt za chvíli dodám :D
Jinak samozřejmě moc díky za všechny rady ;-)
Offline
#2 01. 05. 2013 16:07
- 010010

- Příspěvky: 82
Re: Průběh funkce - kontrola
↑ Katsushiro:
Áno, funkcia nemá lokálne extrémy.
Má práve jeden lokálny extrém, ten je v bode x=0.
Ako vidíme, chyba je v tvojom predpoklade "sudosti".
Druhá derivácia je podľa mňa špatne. Vychádza mi 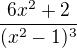 Wol.Alph. taktiež.
Wol.Alph. taktiež.
Offline
#3 02. 05. 2013 21:04
- Katsushiro

- Místo: Rožnov pod Radhoštěm
- Příspěvky: 144
- Škola: VŠB TUO - FEI
- Pozice: student
- Reputace: 2
Re: Průběh funkce - kontrola
↑ 010010:
Samozřejmě máš pravdu, musím si odvyknout to počítání na večer :D
Jen mi není jasný tvoje poznámka ohledně sudosti - tam mám chybu kde? :D
A jinak moc díky ;-)
Offline
#4 02. 05. 2013 21:17
- 010010

- Příspěvky: 82
Re: Průběh funkce - kontrola
↑ Katsushiro:
Mal som na mysli toto: "Tady si nejsem jistý, učili jsme se něco ve smyslu, že pokud je fce sudá/lichá, prostě souměrná, stačí určovat jen jednu polovinu "
Zrejme to nieje pravda. :)
Offline
#5 02. 05. 2013 22:39
- Katsushiro

- Místo: Rožnov pod Radhoštěm
- Příspěvky: 144
- Škola: VŠB TUO - FEI
- Pozice: student
- Reputace: 2
Re: Průběh funkce - kontrola
↑ 010010:
Asi jsem už ke konci semestru úplná lama nebo co, ale proč ne? :D V tom furt problém nevidím, prostě vyřeším st/klesání a konvexnost/konkávnost na jedné straně, a při náčrtu grafu to udělám symetricky na straně druhé, ne? :D
Offline
#6 03. 05. 2013 00:08
- 010010

- Příspěvky: 82
Re: Průběh funkce - kontrola
Áno, nieje to AŽ taký problém. Nakreslil si si tú funkciu ?
Ak je nakreslená správne, musel si zistiť, že ten lokálny extrém tam je.
Ty si ho úvahou sudosti funkcie vynechal, pretože si neuvažoval monotónnosť funkcie na intervale (-1,0) kde je funkcia stúpajúca. Na intervale (0,1) je klesajúca. Funkcia je spojitá v bode 0. Teda x=0 je stacionárny bod, ktorý je zároveň lokálny extrém.
Offline
#7 04. 05. 2013 22:14
Re: Průběh funkce - kontrola
Ahoj, zrovna VŠB ma tady http://www.studopory.vsb.cz/studijnimat … obsah.html
komentovane video, staci vyhledat "prubeh funkce"
Offline
#8 07. 05. 2013 22:20
- Katsushiro

- Místo: Rožnov pod Radhoštěm
- Příspěvky: 144
- Škola: VŠB TUO - FEI
- Pozice: student
- Reputace: 2
Re: Průběh funkce - kontrola
Vřelé díky všem, chtěl jsem tu hodit screen, ale bohužel, zkazil se mi scanner, takže budeme bez obrázku :-( Nicméně ještě jednou díky, snad to pomůže i někomu dalšímu :D
Offline