Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 09. 05. 2013 17:37
Užití goniometrických funkcí
Prosím pomozte s úlohou..
Zadání > Od okraje lesa je vrchol hradeb vidět ve výškovém úhlu 30 stupňů. Od okraje hradního příkopu, který je o 28m blíže k hradbám, je vidět vrchol hradeb ve výškovém úhlu 60 stupňů. Vypočítej výšku hradeb, šířku příkopu a délku nejkratšího žebříku, který by dosáhl od kraje vodního příkopu až na vrchol hradeb.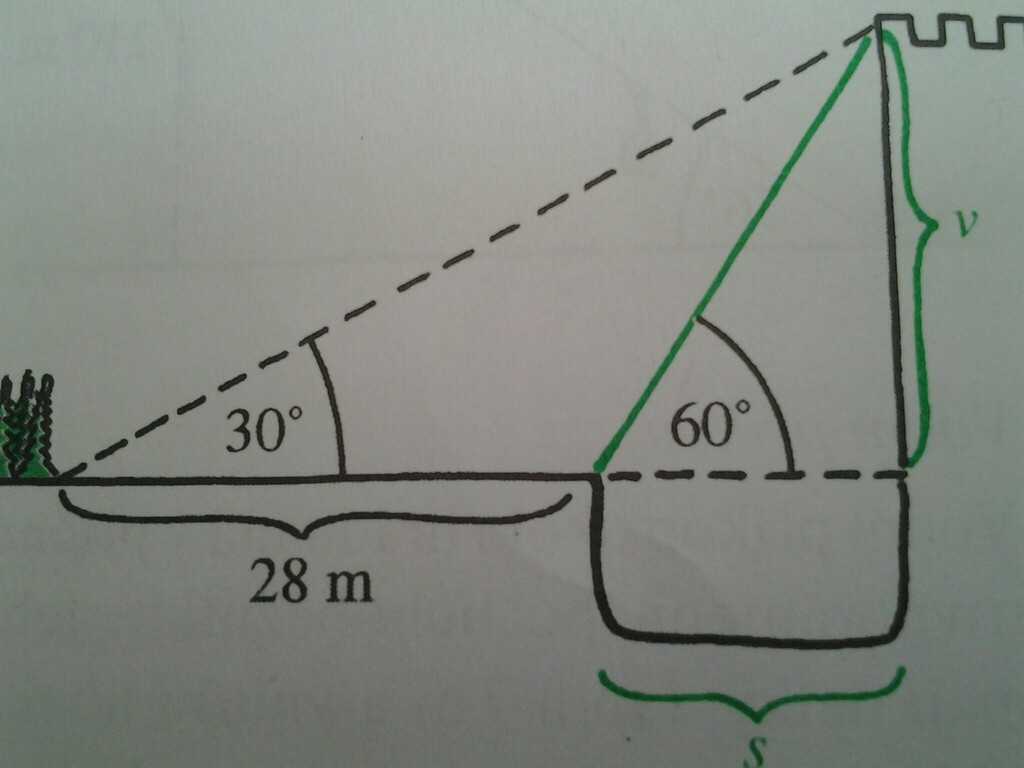
Offline
- (téma jako vyřešené označil(a) terezawho)
#2 09. 05. 2013 17:50
Re: Užití goniometrických funkcí
Trojúhelník "Les, začátek příkopu, vrchol hradeb" je rovnoramenný, protože jeden úhel je 120 a druhý 30. Takže délka žebříku bude stejná jako vzdálenost lesa od začátku příkopu = 28 m.
Potom ten pravoúhlý trojúhelník kde znáš přeponu, tak využiješ goniometrické funkce:
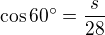
L'Hospitalovo pravidlo neexistuje. Byl to výsledek Johanna Bernoulliho
Offline
#4 09. 05. 2013 19:42
Re: Užití goniometrických funkcí
Tohle byl speciální případ kdy to takhle pěkně vešlo. Kdyby byl ten úhel jiný než 60 (potom by nebylo 120 u toho vedlejsiho) tak by jsi to počítala přes sinovu větu následovně:
A ten úhel alfa by byl vlastně ten poslední (u hradeb nahoře)
L'Hospitalovo pravidlo neexistuje. Byl to výsledek Johanna Bernoulliho
Offline

