Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 13. 05. 2013 14:32
Re: Vzdálenost bodu od přímky
Ahoj ↑ Keeeeke:,
Toto cvicenie mozes vyriesit, vyberom vhodneho reperu priestoru. A tvoj problem je potom jednoduche cvicenie analytickej geometrie.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#3 13. 05. 2013 15:09 — Editoval MirekH (13. 05. 2013 15:09)
Re: Vzdálenost bodu od přímky
↑ Keeeeke:
Pomocí analytické geometrie lze postupovat takto:
BÚNO zvolíme ![kopírovat do textarea $A[0;0;0]$](/mathtex/ef/ef6c5fad77ec36a80076adf6e41ce4b1.gif) a hrany kvádru rovnoběžné s příslušnými osami. Přímku
a hrany kvádru rovnoběžné s příslušnými osami. Přímku  , pro kterou
, pro kterou  , zapíšeme parametricky
, zapíšeme parametricky

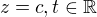
Najdeme kolmici z  na
na  , patou kolmice je bod
, patou kolmice je bod ![kopírovat do textarea $X[at, b - bt, c]$](/mathtex/aa/aa542ef4dfcf6887214d9efe2c371650.gif) . Směrový vektor kolmice
. Směrový vektor kolmice  skalárně vynásobíme s
skalárně vynásobíme s  a požadujeme
a požadujeme 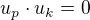 :
:
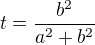
Nyní můžeme vyjádřit![kopírovat do textarea $X = [\frac{ab^2}{a^2 + b^2}; \frac{a^2b}{a^2 + b^2}; c]$](/mathtex/d4/d4c4d4d83854e073aef8778ddba2782f.gif)
a zbývá spočíst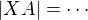
Postup přes pravoúhlé trojúhelníky:
V rovině podstavy máme trojúhelník 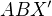 , kde
, kde 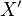 je pata kolmice z
je pata kolmice z  na
na  promítnutá do podstavy. Platí
promítnutá do podstavy. Platí 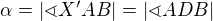 , takže
, takže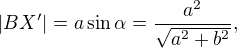


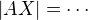
ŘEŠTE FYKOS!
Offline
#6 16. 05. 2013 07:45
Re: Vzdálenost bodu od přímky
↑ Keeeeke:
Např.
Trojúhelník AFH má obsah 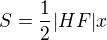
Obsah spočítáš ještě přes Heronův vzorec a porovnáš.
Pořádek je pro blbce, inteligent zvládá chaos!
Offline
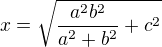 .
.