Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 13. 05. 2013 09:32 — Editoval Keeeeke (13. 05. 2013 11:16)
Vzdálenosti rovin
Ahoj,
je dán kvádr ABCDEFGH s délkami hran AB=BC=a, AE=c. Urči vzdálenost rovin ACF a DEG...
Pohled "kolmý na BD":
kde platí:
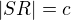
AS...hledaná vzdálenost
Obsah trojuhlenika FSR spocitam dvema zpusoby  - dam do rovnosti a vyjadrim AS. Je to správně?
- dam do rovnosti a vyjadrim AS. Je to správně?
Díky
Offline
- (téma jako vyřešené označil(a) Keeeeke)
#2 13. 05. 2013 16:42
Re: Vzdálenosti rovin
↑ Keeeeke:
Ahoj.
Pomůže nám pohled ve směru společném rovnoběžkám AC, FG , v němž se budou jevit tyto přímky jako body
a roviny , která nás zajímají, jako rovnoběžky procházející po řadě těmito body.
Vzhledem k tomu, že ABCD je čtverec, je tento pohled totožný s kolmým pohledem na rovinu DBF.
Ale nakresleno to máš špatně, například rovina ABD by se měla jevit jako přímka, čemuž Tvůj obrázek neodpovídá
(nebo mu vůbec nerozumím).
Offline
#3 13. 05. 2013 20:17
Re: Vzdálenosti rovin
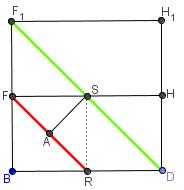
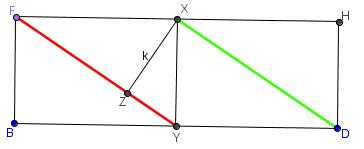
Zkusil jsem to lépe...
Já vím
1-že rovina DEG (zelená) protne usecku FH v půlce (na obrazku bod X)
2-že rovina ACF (červená) protne usecku BD v pulce (na obrazku bod Y)
3-vzdálenost rovin je 
Přitom umím vypočítat:
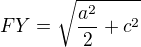

Vypočítám obsah trojuhelniku FXY dvema zpusoby: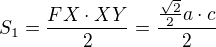

Pote staci vyjadrit  .
.
Je to pochopitelnější? Je to vubec ok?
Díky
Offline
 vede k rovnici s neznámou
vede k rovnici s neznámou