Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 13. 05. 2013 14:08
Vzdálenost mimoběžek
Ahoj, mohli byste mi prosím pomoct vypočítat tento příklad?
Je dána krachle ABCDEFGH, a=4cm. Vypočítejte vzdálenost daných mimoběžných přímek: AC, BH.
Snažila jsem se jimi nějak proložit rovnoběžné roviny, ale nemůžu přijít na to, které to jsou. Děkuji za pomoc :)
Offline
- (téma jako vyřešené označil(a) mark72)
#4 13. 05. 2013 16:28
Re: Vzdálenost mimoběžek
AC je stěnová uhlopříčka dolní podstavy. BH je tělesová uhlopříčka. Musíš vypočítat jeji vzdálenost. Jejich vzdálenost je úsečka kolmá na obě z přímek. Stačí když proložíš přímkou BH rovinu kolmou s dolní podstavou. Vzikne ti obdelník o stranách: a = 4 cm, a*odmocnina ze dvou = 4odmocniny ze dvou.
V tomto obdelníku je přímka BH jedna přímka a ty hledáš vzdálěnost této přímky od bodu S - střed AC.
L'Hospitalovo pravidlo neexistuje. Byl to výsledek Johanna Bernoulliho
Offline
#7 13. 05. 2013 19:35
Re: Vzdálenost mimoběžek
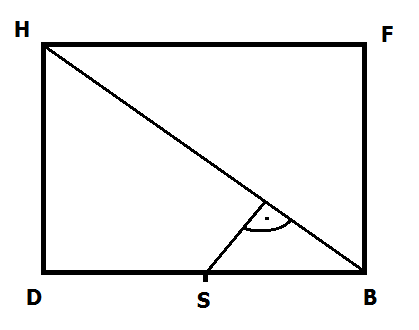
Takže je to vlastně úsečka S - k tomu pravému úhlu. To je hledaná vzdálenost mimoběžek.
Je to pravoúhlý trojúhelník a znáš přeponu (polovina a*odmocnina ze dvou).
Takže teď jde o úhel HBD. Ten spočítáš jednoduše protože je to pravoúhlý trojúhelník. Označme jej alfa.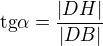

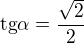
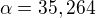
Ta hledaná úsečka je sinus tohoto úhlu krát přepona. Takže:

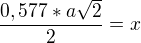
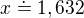
L'Hospitalovo pravidlo neexistuje. Byl to výsledek Johanna Bernoulliho
Offline


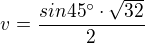 a to je 2, ale správný výsledek
a to je 2, ale správný výsledek