Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 19. 05. 2013 08:28 — Editoval SombreroMickey (19. 05. 2013 08:47)
- SombreroMickey
- Zelenáč
- Příspěvky: 10
- Reputace: 0
Goniometrické rovnice
Dobrý den,
cvičím goniometrické rovnice a našel jsem tři rovnice které mi prostě nevýjdou
1: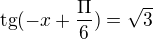
substituce
takže
dále:
y = \frac{\Pi}{3}
Tudíž pro I. kvadrant: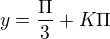
dosadím do substituce:
a výjde:
Což je blbost...
Děkuji za případnou pomoc
Offline
- (téma jako vyřešené označil(a) jelena)
#2 19. 05. 2013 08:42
Re: Goniometrické rovnice
↑ SombreroMickey:
Je to jedna rovnice se dvěma neznámými?
Proč je rovná se v té závorce?
Pořádek je pro blbce, inteligent zvládá chaos!
Offline
#3 19. 05. 2013 08:46
- SombreroMickey
- Zelenáč
- Příspěvky: 10
- Reputace: 0
Re: Goniometrické rovnice
Promiňte, upsal jsem se ...
Offline
#4 19. 05. 2013 09:01
Re: Goniometrické rovnice
↑ SombreroMickey:
Je to dobře až na poslední řádek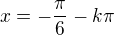
Pořádek je pro blbce, inteligent zvládá chaos!
Offline
#5 19. 05. 2013 09:08 — Editoval SombreroMickey (19. 05. 2013 09:10)
- SombreroMickey
- Zelenáč
- Příspěvky: 10
- Reputace: 0
Re: Goniometrické rovnice
Děkuji za odpověď, ale v učebnici Matematika pro gymnázia Goniometrie mají výsledek: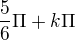
Offline
#6 19. 05. 2013 09:11
- SombreroMickey
- Zelenáč
- Příspěvky: 10
- Reputace: 0
Re: Goniometrické rovnice
Mohu se zeptat s řešením: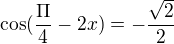
Děkuji mockrát
Offline
#7 19. 05. 2013 09:58
Re: Goniometrické rovnice
↑ SombreroMickey:
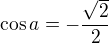
Cosinus je zaporny ve 2. a 3. kvadrantu a proto: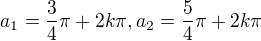
Za a dosadis substituci a dostanes
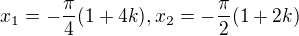
Muzes jeste upravit na zakladni velikosti uhlu: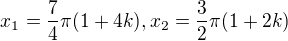
Offline
#8 19. 05. 2013 11:56
Re: Goniometrické rovnice
↑ SombreroMickey: Ten výsledek je stejný. Jenom je posunutý o jedno pí dozadu. Mínus nebo plus kpi už je v podstatě jedno. Záleží jen na tom jaké k budeš dosazovat.
L'Hospitalovo pravidlo neexistuje. Byl to výsledek Johanna Bernoulliho
Offline
#9 19. 05. 2013 12:07
- SombreroMickey
- Zelenáč
- Příspěvky: 10
- Reputace: 0
Re: Goniometrické rovnice
Děkuju moc všem :)
Offline
