Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Konstrukce homomorfismů grup (TOTO TÉMA JE VYŘEŠENÉ)
#1 19. 05. 2013 16:15 — Editoval Hanis (19. 05. 2013 16:21)
- Hanis

- Veterán

- Místo: Brno
- Příspěvky: 2650
- Škola: PřF MUNI - Statistika a analýza dat
- Pozice: Děvče pro všechno
- Reputace: 148
Konstrukce homomorfismů grup
Ahoj :-)
Zadání: Sestrojte všechny homomorfismy 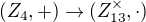
Ahoj,
Generátory 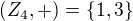
Generátory 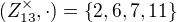
A teď chci stvořit nějaký homomorfismus psí.
Tak neutrální prvek na neutrální:
Generátor na generátor:
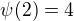

Ale když chci:![kopírovat do textarea $\psi(1)=\psi(5)=\psi(3+2)=8\cdot 4 =[32]_{13}\neq 2$](/mathtex/8a/8a8081ca4939d4e9325c05b6809f539c.gif)
Tak nevím, jaká tam je ještě podmínka... vím, že se to tu na fóru řešilo, ale nějak mi to nejde do hlavy, něco dělám špatně, protože mi to závisí a reprezentantech...
Offline
- (téma jako vyřešené označil(a) Hanis)
#2 19. 05. 2013 16:50
Re: Konstrukce homomorfismů grup
Ahoj ↑ Hanis:,
Ako prve mozes zacat hladat rady vsetkych prvkov v kazdej grupe.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#3 19. 05. 2013 17:46 — Editoval Hanis (19. 05. 2013 17:55)
- Hanis

- Veterán

- Místo: Brno
- Příspěvky: 2650
- Škola: PřF MUNI - Statistika a analýza dat
- Pozice: Děvče pro všechno
- Reputace: 148
Re: Konstrukce homomorfismů grup
V Grupě 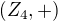 :
: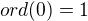
 (generátory)
(generátory)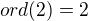
V 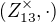
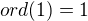
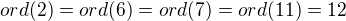
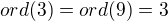



Ale stále mi to není jasné, co kam poslat.
Pokud uvažuju správně, tak generátor musím poslat na generátor. A současně prvky stejného řádu na prvky stejného řádu? To pak ale nepůjde nikdy, protože už generátory mají rozdílný řád...
EDIT:
Ale pokud budu posílat pouze prvky stejného řádu na prvky stejného řádu, tj.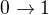
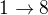
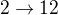

Tak to funguje.
A pro: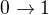

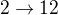
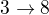
Taky funguje a je vyřešeno. Tedy existují právě 2 homomorfismy, splňující zadání.
Lze to i nějak jednodušeji? Děkuji.
Offline
#4 19. 05. 2013 18:08
Re: Konstrukce homomorfismů grup
↑ Hanis:, jednoduchsie asi nie.... ale toto vyuziva len zakladne vlasnosti a definicie.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#5 19. 05. 2013 18:11
- Hanis

- Veterán

- Místo: Brno
- Příspěvky: 2650
- Škola: PřF MUNI - Statistika a analýza dat
- Pozice: Děvče pro všechno
- Reputace: 148
Re: Konstrukce homomorfismů grup
Děkuji za cennou radu, neměl jsem na mysli složitost co se týče postupu, měl jsem na mysli pracnost a časovou náročnost.
Označuji za vyřešené,
s pozdravem Honza.
Offline
#8 19. 05. 2013 18:34
Re: Konstrukce homomorfismů grup
↑ Andrejka3:,
ano prehliadol som to;
a tiez je aj jeden 4ty, dedinovany tymto 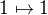
Poznamka:treba pouzit prvky ktorych rad v druhej grupe deli rad prvej, cyklickej grupy.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Konstrukce homomorfismů grup (TOTO TÉMA JE VYŘEŠENÉ)
 ?
?