Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Lineární algebra - Podprostor vektorového prostoru
#1 24. 05. 2013 14:14
Lineární algebra - Podprostor vektorového prostoru
Zdravím,
potřeboval bych poradit s tímto příkladem:
Určete, zda množina V je podprostorem daného lineárního vektorového prostoru. Pokud ano, určete dimenzi tohoto podprostoru V.
1) V prostoru 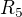 je
je ![kopírovat do textarea $V =\{[x_{1},x_{2},0,0,x_{5}]^{T} | [x_{1},x_{2},x_{5}\in \mathbb{R}\}$](/mathtex/25/25b3dfa42a2d6eb597dd062a662fe42c.gif) .
.
2) V prostoru 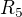 je
je ![kopírovat do textarea $V =\{[x_{1},x_{2},2,x_{4},x_{5}]^{T} | [x_{1},x_{2},x_{4},x_{5}\in \mathbb{R}\}$](/mathtex/0c/0c94e3728fa0829b497bdb01d84e6fa7.gif) .
.
Děkuji za pomoc! :)
Offline
#2 24. 05. 2013 14:36
Re: Lineární algebra - Podprostor vektorového prostoru
Ahoj ↑ honyik:,
1)
Ako prve mozes dokazat ze ![kopírovat do textarea $[1;0;0;0;0] ^ T;[[0;1;0;0;0]^ T;[0;0;0;0;1]^ T$](/mathtex/37/3734a36f6daf3d57d8f6a0a415bf55d4.gif) je baza V
je baza V
2) ukaz, ze ![kopírovat do textarea $[0;0;0;0;0]^ T$](/mathtex/93/9386c03f8c10f4ff0c97b86bd0b0fec6.gif) nie je v V.... Co znamena......
nie je v V.... Co znamena......
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#4 24. 05. 2013 15:10
Re: Lineární algebra - Podprostor vektorového prostoru
To pises o 1)
Ten tvoj zapis sa da interpretovat ako riesenie urciteho systemu, a to da ze je mozne napisat jedinym sposobom nulovy vektor.... A na koniec ze tie tri vektory co som napisal vyssie su LN
A ako ukazes ze generuju V?
Poznamka: tvoj pristup ukazuje, ze si uz dost studoval tieto pojmy, ale musis sa zlepsit aby si to dokazal jasne vyjadrit.
À co otazka 2) ?
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#5 24. 05. 2013 15:32
Re: Lineární algebra - Podprostor vektorového prostoru
1) No to bych ukázal, tak že bych si vypočítal hodnost, která je 3, ale dimenze je 5? Takže ji negenerují?
2) Tomuhle nerozumím, spíš nevím co tím myslíš a jak na to?
Děkuji za pomoc! :)
Offline
#6 24. 05. 2013 16:04 — Editoval Rumburak (25. 05. 2013 11:24)
Re: Lineární algebra - Podprostor vektorového prostoru
↑ honyik:
Ahoj.
Kolega ↑ vanok: tu momentálně není přihlášen, tak se pokusím odpovědět za něho.
K otázce č. 1 je důležité si uvědomit, že pro libovolná  je
je
![kopírovat do textarea $[x_{1}, x_{2}, 0, 0, x_{5}]^{T} = x_1 [1 , 0, 0, 0 , 0]^{T} + x_2 [0 , 1, 0, 0 , 0]^{T} + x_5 [0 , 0, 0, 0 , 1]^{T}$](/mathtex/db/db964fc594c77ee56e6ccba88862d02f.gif) ,
,
při čemž vektory ![kopírovat do textarea $ [1 , 0, 0, 0 , 0]^{T} , [0 , 1, 0, 0 , 0]^{T} , [0 , 0, 0, 0 , 1]^{T}$](/mathtex/46/46ce17fb396a86e78e8d9df49d51a08e.gif) jsou lineárně nezávislé.
jsou lineárně nezávislé.
K otázce č. 2 je důležité si uvědomit, že každý podprostor vektorového prostoru W m.j. obsahuje nulový vektor prostoru W ,
což v případě prostoru 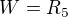 je vektor
je vektor ![kopírovat do textarea $[0 , 0, 0, 0, 0]^T$](/mathtex/ec/ec98c325c7d8346e281299e0516b8e34.gif) .
.
Offline
#7 24. 05. 2013 16:05 — Editoval vanok (24. 05. 2013 16:05)
Re: Lineární algebra - Podprostor vektorového prostoru
Tie tri vektory su baza V.
Uz vies ze su LN.
À naviac mas ![kopírovat do textarea $[ x_1; x_2;0;0; x_3]^ T=x_1[1;0;0;0;0] ^ T+ x_2[0;1;0;0;0]^ T+ x_3[0;0;0;0;1]^ T$](/mathtex/be/bee2f488c3da366778d91c0d96f0395e.gif) , co znamena ze V je generovane z
, co znamena ze V je generovane z![kopírovat do textarea $[1;0;0;0;0] ^ T;[[0;1;0;0;0]^ T;[0;0;0;0;1]^ T$](/mathtex/37/3734a36f6daf3d57d8f6a0a415bf55d4.gif) !
!
Mas pravdu ze povodny priestor ma dim 5, à toto ukazuje, ze V ma dim 3.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#8 24. 05. 2013 16:07
Re: Lineární algebra - Podprostor vektorového prostoru
2)kazdy podpriestor obsahuje nulovy vektor, ale tento ho nema, cize....
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#9 24. 05. 2013 16:09 — Editoval vanok (24. 05. 2013 16:38)
Re: Lineární algebra - Podprostor vektorového prostoru
Pozdravujem ↑ Rumburak:,
Zaroven piseme a to iste. Ako sa hovori Velki duchovia sa casto stretnu.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#12 25. 05. 2013 10:32
Re: Lineární algebra - Podprostor vektorového prostoru
↑ honyik:,
To preto, lebo V obsahuje vylucne prvky, ktorych tretia suradnica musi byt 2. ( nulovy vektor, ma vsetki suradnice nulove, tak pochopitelne aj tu tretiu)
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#15 25. 05. 2013 13:36
Re: Lineární algebra - Podprostor vektorového prostoru
Jo aha, takže pro rekapitulaci prvního příkladu:![kopírovat do textarea $V =\{[x_{1},x_{2},0,0,x_{5}]^{T} | x_{1},x_{2},x_{5}\in \mathbb{R}\}$](/mathtex/a7/a718ad98076679ac3d4c03639085be0f.gif)
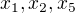 mi udávají, že hledám nulový vektor
mi udávají, že hledám nulový vektor ![kopírovat do textarea $[x_{1},x_{2},x_{3}] = [0,0,0]$](/mathtex/1b/1b6973c90bf55837f705156a4da49219.gif) .
.
To splňuje a znamená, že je to podprostor. Proto si vemu vektory ![kopírovat do textarea $ [1,0,0,0,0]^{T} , [0,1,0,0,0]^{T},[0,0,0,0,1]^{T}$](/mathtex/ca/ca7918c3e65fd6f306497384c691a900.gif) , abych si vypočítal dimenzi podprostoru a dám do matice.
, abych si vypočítal dimenzi podprostoru a dám do matice.
1 0 0 | 0
0 1 0 | 0
0 0 0 | 0
0 0 0 | 0
0 0 1 | 0
Z toho vidím, že ![kopírovat do textarea $[1,0,0,0,0]^{T} , [0,1,0,0,0]^{T},[0,0,0,0,1]^{T}$](/mathtex/65/65ebfed8221c43ea9503fdf4fa5254c1.gif) jsou báze V a dim V = 3.
jsou báze V a dim V = 3.
Děkuji za pomoc! :)
Offline
#16 25. 05. 2013 14:13 — Editoval Rumburak (25. 05. 2013 14:24)
Re: Lineární algebra - Podprostor vektorového prostoru
↑ honyik:
Snad to myslíš dobře, ale to, co jsi teď napsal, je matamatickému vyjadřování velmi vzdáleno :-) a tudíž nesrozumitelné.
V první úloze se žádný nulový vektor hledat nemusí. Prostě vztah
![kopírovat do textarea $[x_{1}, x_{2}, 0, 0, x_{5}]^{T} = x_1 [1 , 0, 0, 0 , 0]^{T} + x_2 [0 , 1, 0, 0 , 0]^{T} + x_5 [0 , 0, 0, 0 , 1]^{T}$](/mathtex/db/db964fc594c77ee56e6ccba88862d02f.gif)
platný právě pro pro každý vektor ![kopírovat do textarea $[x_{1}, x_{2}, 0, 0, x_{5}]^{T} \in V$](/mathtex/23/23f3277c3fbc49bb979b70d5c0ef4464.gif) (platný na základě definic lineárních operací v
(platný na základě definic lineárních operací v 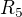 , čemuž bys měl rozumět)
, čemuž bys měl rozumět)
říká, že  je lineárním obalem vektorů
je lineárním obalem vektorů
(1) ![kopírovat do textarea $ [1 , 0, 0, 0 , 0]^{T} , [0 , 1, 0, 0 , 0]^{T} , [0 , 0, 0, 0 , 1]^{T}$](/mathtex/46/46ce17fb396a86e78e8d9df49d51a08e.gif)
(tudíž podprostorem v 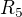 , odkud vektory (1) jsou ).
, odkud vektory (1) jsou ).
Vektory (1) tedy představují systém generátorů (pod)prostoru  - navíc jsou lineárně nezávislé (to bys měl vědět, není těžké to dokázat) a proto
- navíc jsou lineárně nezávislé (to bys měl vědět, není těžké to dokázat) a proto
můžeme říci, že tento systém generátorů (pod)prostoru  je jeho bází. Platí věta, že všechny možné báze téhož vekt. prostoru mají stejný počet prvků,
je jeho bází. Platí věta, že všechny možné báze téhož vekt. prostoru mají stejný počet prvků,
toto číslo se nazývá dimensí onoho prostoru. V případě (pod)prostoru  je toto číslo rovno 3, protože jeho báze (systém (1)) má 3 prvky.
je toto číslo rovno 3, protože jeho báze (systém (1)) má 3 prvky.
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Lineární algebra - Podprostor vektorového prostoru

![kopírovat do textarea $V =\{[x_{1},x_{2}, \fbox{2},x_{4},x_{5}]^{T} | x_{1},x_{2},x_{4},x_{5}\in \mathbb{R}\}$](/mathtex/83/83d38903d29a6d0f5818194242ea03df.gif) z úlohy 2 stanoví, že pro libovolný vektor
z úlohy 2 stanoví, že pro libovolný vektor![kopírovat do textarea $[x_{1},x_{2},x_3,x_{4},x_{5}]^{T} \in V$](/mathtex/c1/c1223f84290d88b074e22780896bacb9.gif) je
je 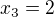 , tuto podmínku však nulový vektor
, tuto podmínku však nulový vektor ![kopírovat do textarea $[0, 0, 0, 0, 0]^{T}$](/mathtex/35/357d5427bedd17b748604c2cf1ad7b6a.gif) nesplňuje ,
nesplňuje , ![kopírovat do textarea $[0, 0, 0, 0, 0]^{T}\notin V$](/mathtex/48/488bb03066d6141cde65e9b20823c6b7.gif) .
.