Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 25. 05. 2013 17:00 — Editoval honyik (25. 05. 2013 17:06)
Lineární algebra - vektorový prostor
Zdravím,
potřeboval bych poradit s tímto příkladem, spíš mám problém s tím, že nevím co počítám:
Ukažte, že prvky tvoří bázi prostoru  . Ukažte, že prvek
. Ukažte, že prvek 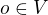 a určete ô souřadnice prvku
a určete ô souřadnice prvku 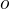 v této bázi. (Místo
v této bázi. (Místo 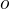 má být
má být  , ale nepodařilo se mi udělat vakoň nad z.)
, ale nepodařilo se mi udělat vakoň nad z.)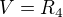
![kopírovat do textarea $r_{1}=[2,0,-1,1]^{T}$](/mathtex/e7/e728b336ff93bbad485e7b8fa5800885.gif)
![kopírovat do textarea $r_{2}=[1,-3,1,0]^{T}$](/mathtex/f1/f109a6894c76b01fb09520dfafa03a58.gif)
![kopírovat do textarea $r_{3}=[-3,2,0,5]^{T}$](/mathtex/f8/f8c966e01c59053a4f65392beb418b6b.gif)
![kopírovat do textarea $r_{4}=[0,-2,1,1]^{T}$](/mathtex/ac/ace20e12284781564113d35da36f108a.gif)
![kopírovat do textarea $o=[0,-5,2,8]^{T}$](/mathtex/ce/ce14c143ce765e46d81ce47e1c2f2f12.gif)
____________________________________________________
Mám vypočítat bázi, tedy vemu vektory a poskládám do matice.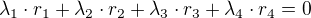
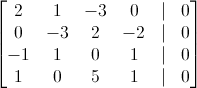
Po úpravách mi vyjde: 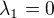 ,
, 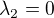 ,
, 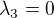 a
a 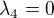
To znamená, že vektory jsou LN a tvoří bázi  .
.
A odtud nevím, co počítám, vím jen, že vypočítám souřadnice ô.
Jelikož všechny vektory jsou bázové, tak je zase poskládám do rozšířené matice o "o".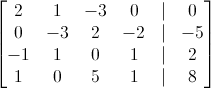
Po úpravách mi vyjde, že: ô![kopírovat do textarea $=[1,1,1,2]^{T}$](/mathtex/96/96aed86da4fdc36164df469382159194.gif)
No mám bázi a vypočítané souřadnice, ale jak mám určit prvek 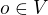 ?
?
Děkuji za pomoc! :)
Offline
#2 26. 05. 2013 01:03
Re: Lineární algebra - vektorový prostor
Podle všeho je vektor (1,1,1,2) výsledek. Jedná se o souřadnice vektoru o vzhledem k zadané bázi.
lektornamiru.cz- doučování na pro Vás
Offline
#3 26. 05. 2013 09:04
- OiBobik

- Moderátor

- Místo: Brno/Praha
- Příspěvky: 1013
- Škola: MFF UK Mat. struktury
- Pozice: student
- Reputace: 82
Re: Lineární algebra - vektorový prostor
↑ honyik: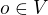 už plyne z toho, že
už plyne z toho, že 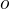 má vůbec nějaké souřadnice k dané bázi
má vůbec nějaké souřadnice k dané bázi
(vektor  má souřadnice
má souřadnice  vzhledem k bázi
vzhledem k bázi 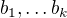 z definice právě tehdy, když
z definice právě tehdy, když 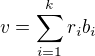 , spec. je tedy
, spec. je tedy 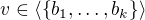 ).
).
"The first rule of Tautology Club is the first rule of Tautology Club." [xkcd]
Offline