Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 28. 05. 2013 18:54
- nejsem_tonda

- Příspěvky: 649
- Reputace: 54
Re: Odchylka rovin
Ahoj,
analyticky.
(Souradnice bodu se zvladnou a normalove vektory rovin nasledne taky.)
Offline
#3 28. 05. 2013 18:56
Re: Odchylka rovin
↑ Keeeeke:
Ahoj,
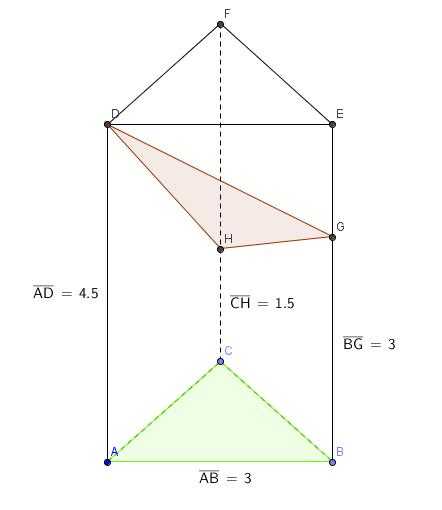
počítal bych to nejspíš jako úhel normálovývh vektorů těch dvou rovin. Zvolil bych si souřadnou soustavu xyz tak, aby xy byla vodorovná rovina s osou x = AB. Normálový vektor podstavy je n_1 = (0,0,1). Dále bych si určil souřadnice vektorů DH, DG a normálový vektor té druhé roviny je pak n_2= DH x DG.
Wolfram ani jiný chemický prvek matematiku nenaučí.
Offline
#5 28. 05. 2013 22:03
- nejsem_tonda

- Příspěvky: 649
- Reputace: 54
Re: Odchylka rovin
No vzhledem k tomu, ze to vychazi pekne, tak to jde, ale prijde mi dost prirozene odpovidat na tyhle otazky analyticky.
Misto odchylky rovin DHG a ABC se budu divat na odchylku rovin DHG a DEF (zadny trik, jenom bych jinak musel oznacovat vic bodu). Kdyz  dvakrat prodlouzim, dostanu se do tehoz bodu jako kdyz dvakrat prodlouzim
dvakrat prodlouzim, dostanu se do tehoz bodu jako kdyz dvakrat prodlouzim  , protoze HF je dvakrat delsi nez GE. Oznacime tento bod I odted budu pocitat odchylku rovin DHI a DEF.
, protoze HF je dvakrat delsi nez GE. Oznacime tento bod I odted budu pocitat odchylku rovin DHI a DEF.
Ted bych chtel najit rovinu kolmou jak na DEF, tak i na DHI. Roviny kolme na DEF je snadne si predstavit a ja z nich chci vybrat tu spravnou. Predstavuju si roviny kolme na DEF, ktere prochazeji bodem F. Jenom jedna z techhle moznych rovin bude kolma na DI a protoze urcite existuje jedna rovina, ktera je kolma na DEF i na DHI, tak to bude prave ta, ktera je kolma na DI. A ja tvrdim, ze primo DF je kolme na DI. Proc? Protoze bod E je stejne vzdaleny od bodu F, D i I, takze kdybychom sestrojili Thaletovu kruznici nad prumerem FI, bude tato kruznice prochazet bodem D. Tim jsme teda zjistili, ze ta spravna kolma rovina na DEF, ktera je kolma i na DHI, je rovina obsahujici DF, cili primo stena DFH!
No a uhodnout odchylku DF a DH je sranda, kdyz DF a FH jsou stejne dlouhe a na sebe kolme.
Mozna to jde nejak jednoduseji, ale po chvili premysleni me nic jednodussiho nenapadlo...
Offline