Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 06. 06. 2013 22:32
Povrch koule
Dobrý den, hledal jsem všude, jak tady na fóru, tak na googlu a prostě jediné co jsem našel (a to mi bylo dost k ničemu) na anglické wikipedii kde napsali že povrch koule je první derivace vzorce pro objem koule.
Ten odvodit umím ale ten povrch jsem nikde nenašel. Proč je to vůbec derivace objemu? Byl by schopný mi to tady krok po kroku odvodit?
Můj profesor na matematiku mi nebyl schopný nic k tomu říct. Jediné co jsem se dozvěděl že se to dělá přes integrál, to vím taky no :D ale jak? (spíš to odvození přes integrál, než nějaky archimedovsky pokusy s poměrem válce kužele apodobně)
Doufám že se někdo najde, kdo tohle zná.
Děkuju
L'Hospitalovo pravidlo neexistuje. Byl to výsledek Johanna Bernoulliho
Offline
#2 06. 06. 2013 22:52
#4 07. 06. 2013 20:06
- Jan Jícha

- Veterán

- Místo: Plzeň/Mnichov
- Příspěvky: 1801
- Škola: ZČU - FST - KMM
- Pozice: Safety Engineer
- Reputace: 74
- Web
Re: Povrch koule
Někde jsem viděl ještě zajímavý odvození pro objem - trochu netradiční.
Než kalkulovat s integrály, Archimédes přišel na to, že pokud do válce o výšce 2r a poloměru r, vložím kouli o poloměru r, vyteče nám 2/3 objemu vody, a že tedy poměr objemu koule ku objemu válce je 2/3
Objem válce je tedy 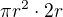 a objem koule je tedy
a objem koule je tedy 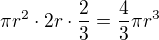
Offline
#5 07. 06. 2013 20:23
Re: Povrch koule
Jojo, přesně o tomhle sem mluvil s tím archimedem. To byl zajímavy pokus ale kdyby to náhodou bylo třeba o 1/1000 jinak tak už by to bylo špatně. Každopádně sem sám překvapenej že je to takhle přesně i když to je vlastně tou konstantou pí
L'Hospitalovo pravidlo neexistuje. Byl to výsledek Johanna Bernoulliho
Offline
#6 07. 06. 2013 20:28
- Jan Jícha

- Veterán

- Místo: Plzeň/Mnichov
- Příspěvky: 1801
- Škola: ZČU - FST - KMM
- Pozice: Safety Engineer
- Reputace: 74
- Web
Re: Povrch koule
Ještě přidám zajímavý odkaz http://www.walter-fendt.de/m14cz/kugelvolumen_cz.htm
Offline
#7 07. 06. 2013 21:08
Offline