Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 29. 06. 2013 18:40
- miso16211
- Πυθαγόραc
- Příspěvky: 1522
- Pozice: n/a
substitučná metoda - znak dx
nechápem, prečo sa len tak z vyrazu 
môže len tak pripisat dalsie x do sucinu. ved dx je len určovaci znak, hovori o tom ze hladam derivaciu s neznamou x. Je dx sučin?
Offline
- (téma jako vyřešené označil(a) miso16211)
#2 29. 06. 2013 19:15
- teolog


- Místo: Praha
- Příspěvky: 3498
- Škola: MFF + PřF UK
- Pozice: Gymnázium Přírodní škola - učitel (M, Z)
- Reputace: 167
Re: substitučná metoda - znak dx
↑ miso16211:
Zdravím,
dx není součin, je to jen označení neznámé, podle které se integruje.
Offline
#3 29. 06. 2013 20:46 — Editoval miso16211 (29. 06. 2013 20:49)
- miso16211
- Πυθαγόραc
- Příspěvky: 1522
- Pozice: n/a
Re: substitučná metoda - znak dx
↑ teolog:
tak ako je možné, že podľa nej derivujem. ak si zadefinujem napr. t= 2x
tak sa mi zobrazi v predpise integralu 2 v súčine.
nie je to náhodou niečo ako toto? 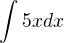 =
=  čize je to násobenie derivaciou x a zaroveň pomôcka, podľa ktorej vie ten kto to počíta, čo je neznáma?
čize je to násobenie derivaciou x a zaroveň pomôcka, podľa ktorej vie ten kto to počíta, čo je neznáma?
Offline
#4 29. 06. 2013 21:33 — Editoval JohnPeca18 (29. 06. 2013 21:41)
- JohnPeca18

- Příspěvky: 651
- Škola: MFF UK
- Pozice: Absolvent 2014
- Reputace: 81
Re: substitučná metoda - znak dx
No podla mojej vedomosti 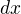 je diference x, a tým se myslí "mala" zmena v hodnote x. Integrál je teda ako suma cez male rozdili v hodnote x, videt to v tom jak se vysvetluje integral ako obsah plochy pod funkciou, s tym, ze se scitaji strasne uzke sloupce sirky dx, a vysky
je diference x, a tým se myslí "mala" zmena v hodnote x. Integrál je teda ako suma cez male rozdili v hodnote x, videt to v tom jak se vysvetluje integral ako obsah plochy pod funkciou, s tym, ze se scitaji strasne uzke sloupce sirky dx, a vysky  a proto je to zapsané ako v soucinu
a proto je to zapsané ako v soucinu  . A derivácia to je zase pomer "malych zmen" v funkci f(x) k "malym zmenam" x, teda
. A derivácia to je zase pomer "malych zmen" v funkci f(x) k "malym zmenam" x, teda 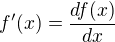
Tak aspon, ja tomu tak rozumiem.
Potom aj substitucna metoda sa sa da vyjadrit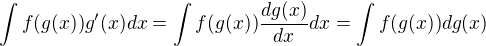
a ze substituce 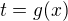
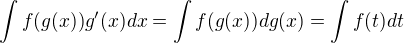
Offline
#5 29. 06. 2013 21:41
Re: substitučná metoda - znak dx
↑ miso16211:
Ahoj,
JohnPeca podal pěkné vysvětlení, akorát bych neříkal diference, nicméně diferenciál. Já bych ještě rád ukázal ten rozdíl oproti diferenci, který by ti měl ukázat, jak ten integrál jako takový funguje.
Pokud máme nějaké prvky  , potom jejich lineární kombinací dostaneme
, potom jejich lineární kombinací dostaneme 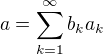 ,
,
přičemž uvažujme nyní, že hodnoty 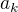 jsou hodnoty nějakého rozdílu, třeba
jsou hodnoty nějakého rozdílu, třeba  , tedy to označíme
, tedy to označíme 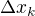 a nazveme diferencí
a nazveme diferencí  , máme tedy v závislosti na
, máme tedy v závislosti na  novou funkci
novou funkci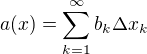 .
.
Tímhle se dostáváme k určitému spočtenému součtu. Pokud by však byl součet nespočetný (třeba přes reálná čísla), pak často nahrazujeme součet (sumu) integrací, když právě uvažujeme, že diference jde k nule, tj. 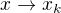 . Proto dostáváme
. Proto dostáváme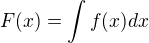 ,
,
kdy  je funkce, která popisuje spojité rozložení výše uvedených indexů
je funkce, která popisuje spojité rozložení výše uvedených indexů  . Potom
. Potom 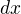 má, jak psal kolega, význam hrozmě malinkaté změny (jdoucí do nuly). Jedná se tedy o součin
má, jak psal kolega, význam hrozmě malinkaté změny (jdoucí do nuly). Jedná se tedy o součin 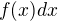 , ovšem
, ovšem 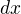 už není součin žádného samostatného d a x, jedná se o samostatnou veličinu označující infinitezimální změnu dx.
už není součin žádného samostatného d a x, jedná se o samostatnou veličinu označující infinitezimální změnu dx.
To, co jsem napsal, není úplně správně v tom smyslu matematické přesnosti, ale já si to takhle rád představuji, protože mi to přijde dost ilustrační. Snad tedy tím pomohu i tobě.
S pozdravem
J.
Což je to možné! Tento stařičký světec ještě ani nezaslechl v svém lese, že bůh je mrtev!
Offline