Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 16. 07. 2013 10:01 — Editoval OiBobik (16. 07. 2013 10:06)
- OiBobik

- Moderátor

- Místo: Brno/Praha
- Příspěvky: 1013
- Škola: MFF UK Mat. struktury
- Pozice: student
- Reputace: 82
Re: Tečný bandl S^2
↑ Honza90:
Ahoj,
předpokládám, že  je klasická 2-dim sféra v
je klasická 2-dim sféra v 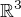 , tj.
, tj.  .
.
No tak pak je tečný bandl (stejně jako obecně tečný bandl variety) zkrátka disjunktní sjednocení tečných prostorů v jednotlivých bodech, ne?
Tedy něco jako ,
,
kde kolmení je vzhledem ke standardnímu skalárnímu součinu,
s projekcí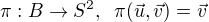 .
.
Podrobněji a obecněji na Wiki.
"The first rule of Tautology Club is the first rule of Tautology Club." [xkcd]
Offline
#3 16. 07. 2013 22:17
Re: Tečný bandl S^2
↑ OiBobik:
Jde o to jestli jak jsi to napsal je to izomorfni s  , coz byt nemuze kvuli tomu ze na sfere neni spojite nonvanishing vektorove pole. Vim ze je to zmatene, sam tomu poradne nerozumim.
, coz byt nemuze kvuli tomu ze na sfere neni spojite nonvanishing vektorove pole. Vim ze je to zmatene, sam tomu poradne nerozumim.
Wir müssen wissen. Wir werden wissen. David Hilbert
Offline