Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Diferenciální rovnice (TOTO TÉMA JE VYŘEŠENÉ)
#2 10. 07. 2013 17:45
Offline
#3 10. 07. 2013 17:57
Re: Diferenciální rovnice
↑ frantax:Já bych tuto DR řešil substitucí z=y/x,pak y'=z'*x+z Zadání upravím takto:y'=(1+z)/(1-z).Za y' dosadím výraz ze substituce a po lehké úpravě dostanu:Integrál(1+z)/(1+z^2)dz=Integrál1/xdx,což řeším standartním způsobem.Stačí?
Matematika je způsob,jak zviditelnit neviditelné!!
Offline
#7 10. 07. 2013 20:40 — Editoval Jj (10. 07. 2013 20:44)
Re: Diferenciální rovnice
↑ frantax:
Výsledek podle MAWu se dá upravit na Váš výsledek užitím vztahů 
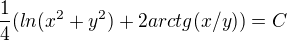


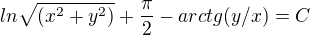



Takže je to podle mne v pořádku.
Pokud se tedy nemýlím.
Offline
#9 12. 07. 2013 13:32 — Editoval jelena (14. 07. 2013 09:36)
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Diferenciální rovnice
Zdravím v tématu,
jen můj názor k úpravám MAW. MAW je stroj a má zabudované strojové úpravy, co by asi člověk rovnou neprováděl. Tedy osobně bych použila z odkazu MAW předposlední řádek před konečnou úpravou a zkoušku bych provedla pomocí derivace (zde je výsledek "funkce v implicitním tvaru") a dosazování do původní rovnice. A to jak "můj" výsledek, tak i MAW.
Spíš bych se zeptala někoho z kolegů - ve výsledku napravo musí být absolutní hodnota =ln|x|+C. Za jakých podmínek se potom upraví, že absolutní hodnota není? Moc děkuji.
EDIT: tato úprava snad odstraňuje absolutní hodnotu "bez rizika":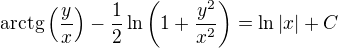 *2
*2
 tak absolutních hodnot už není třeba.
tak absolutních hodnot už není třeba.
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Diferenciální rovnice (TOTO TÉMA JE VYŘEŠENÉ)
 - Rovnice
- Rovnice - Obecne reseni
- Obecne reseni![kopírovat do textarea $arctg(y/x)-ln(\sqrt[2]{\frac{x^2+y^2}{x^2}}-ln(x)=C$](/mathtex/b4/b4eb4404bfd9f69dadf5b934a5b8cfcb.gif)
![kopírovat do textarea $arctg(y/x)+ln(\frac{1}{\sqrt[2]{\frac{x^2+y^2}{x^2}}}*\frac{1}{\sqrt{x^2}})=C$](/mathtex/4d/4d411fc94f33269e184df5da574db805.gif)
![kopírovat do textarea $arctg(y/x)+ln(\frac{1}{\sqrt[2]{x^2+y^2}})=C$](/mathtex/10/1005b8d7ac7329311dca2998fec62b42.gif)
