Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 25. 05. 2013 14:27
pocet delitelov
Tento krat tu davam, jedno trocha tazsie cvicenie.
No som si isty, ze sa bude pacit viacerym foristom.
Nech 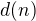 oznacuje pocet vsetkych prirodzenych delitelov cisla
oznacuje pocet vsetkych prirodzenych delitelov cisla  ,
,
ich sucet oznacime  ;
; 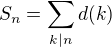 .
.
Priklady: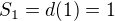
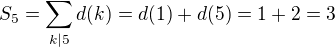
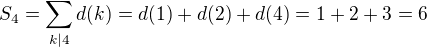
A) dokazte, ze 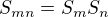 pre nesudelitelne
pre nesudelitelne 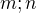
B) urcite  take, ze
take, ze 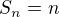
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#2 26. 06. 2013 18:45
Re: pocet delitelov
Cast A) je jednoducha, nikto si to nechce skusit?
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#3 28. 07. 2013 11:50
Re: pocet delitelov
Offline
#4 28. 07. 2013 19:43 — Editoval vanok (28. 07. 2013 19:58)
Re: pocet delitelov
Pozdravujem ↑ Brano:,
Este mame jedno riesenie: 36.
Zaujima ta aj moje podrobne riesenie?
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#5 28. 07. 2013 23:29
Re: pocet delitelov
Aha ano, ja som postupoval cez moznosti 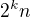 pre
pre  neparne a preskusal som
neparne a preskusal som 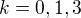
 bolo uz lahke a
bolo uz lahke a 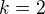 som tak nejak odmavol rukou, ze tam uz nic nebude a predsa potvora :-)
som tak nejak odmavol rukou, ze tam uz nic nebude a predsa potvora :-)
Moje riesenie bolo dost zdlhave, aj ked nie velmi komplikovane - preto som ani poriadne nedokoncil, ani sa mi ho nechcelo pisat.
Ale zaujimalo by ma ci si tam mal nejaku inu myslienku, alebo ci to bolo v podstate to iste. Tak ho nemusis nutne napisat podrobne - staci naznak.
Offline
#6 29. 07. 2013 01:12 — Editoval vanok (29. 07. 2013 01:13)
Re: pocet delitelov
ok, tak strucne:
Zda sa mi ze sme to robili velmi podobne ( no pridam nejake detaily)
Okamzite n=1 vyhovuje
Ak n=p (prvocislo), len p=3 vyhovuje
Pripad 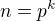 da ze riesenie nemoze existovat;
da ze riesenie nemoze existovat;
vdaka vysetreniu funkcie 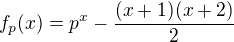
ktora je ostro rastuca pre 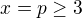
A jej studium pre  a
a 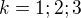 a pre
a pre 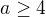 ukaze, ze nemoze byt nula, co ukaze ze hladana rovnost je nemozna v tomto pripade.
ukaze, ze nemoze byt nula, co ukaze ze hladana rovnost je nemozna v tomto pripade.
Pre 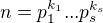 sa lahko ukaze, ze je nemozne a vsetky
sa lahko ukaze, ze je nemozne a vsetky  boli
boli 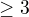
preto riesenie musi byt formy 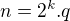 ( q neparne )
( q neparne )
A ani ja som velmi neformalizoval tento pripad...
a pri hladani riesenia som pouzil maximum tohto vyrazu 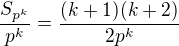
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline

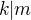 a
a 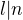 potom
potom 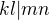 naviac ak
naviac ak 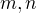 su nesudelitelne potom ak
su nesudelitelne potom ak 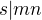 , tak
, tak 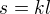 take, ze
take, ze  a
a  su nesudelitelne, potom
su nesudelitelne, potom 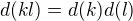 .
.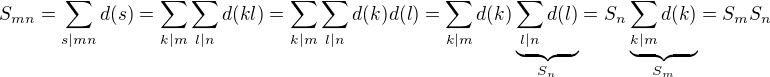
 vyraz
vyraz a sice nie az tak rychlo ale predsa aj s rastucim
a sice nie az tak rychlo ale predsa aj s rastucim 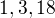 .
.