Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Matice lineárního operátoru (TOTO TÉMA JE VYŘEŠENÉ)
#1 15. 09. 2013 16:30
Matice lineárního operátoru
Dobrý den, prosím, mohl by mi někdo poradit s tímto příkladem se zadáním b) ? U kanonické báze je mi jasné, jak postupovat, ale jak vytvořit tu matici lin. operátoru s touhle bází, na to pořád nemůžu přijít. Zkoušela jsem dosazovat jako v případě kanonické báze, tj. L(q1) = L(x^2 + x + 1) = (-2 + 5 + 1)x^2 + (5 - 3 - 5)x + (-4 + 5 + 6), ale to je asi špatně, co? Každopádně se mi takhle nepodařilo dojít k výsledku (výsledek znám). 
Offline
- (téma jako vyřešené označil(a) nanny1)
#2 15. 09. 2013 17:13
Re: Matice lineárního operátoru
Ahoj ↑ nanny1:,
Tvoj vypocet  je skoro dobry, len si tam zabudol 4 pred
je skoro dobry, len si tam zabudol 4 pred  . (4c... A nie c)
. (4c... A nie c)
Ale vysledok potom musis vyjadrit v baze. 
Tak pokracuj.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#3 15. 09. 2013 18:11 — Editoval nanny1 (15. 09. 2013 20:24)
Re: Matice lineárního operátoru
↑ vanok:
Děkuju. :) Takže jestli to správně chápu, mělo by to být: 


Vím, že matice A bude po sloupcích složená ze souřadnicových vektorů L(q1), L(q2) a L(q3). V kanonické bázi jsou vektory totožné s obrazy L(qi), u tohohle tápu.. Souřadnicové vektory se určovaly jako matice s pravou stranou, kde matice byla složená z prvků báze a pravá strana byl vektor, jehož souřadnice jsem chtěla vypočítat. Jde se tady na to nějak podobně? Pravá strana budou postupně ty báze qi?
Offline
#4 15. 09. 2013 21:17
Re: Matice lineárního operátoru
Otazka b)
Cize najprv treba vyjadrit 3 najdene obrazy vektorov  ako linearnu kombinaciu vektorov
ako linearnu kombinaciu vektorov 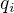 .
.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Matice lineárního operátoru (TOTO TÉMA JE VYŘEŠENÉ)


 , vyřeším soustavu rovnic a řešení je první sloupec matice lineárního zobrazení a tak dál..
, vyřeším soustavu rovnic a řešení je první sloupec matice lineárního zobrazení a tak dál..