Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Graf nezahrnuje spodní hemisféru (TOTO TÉMA JE VYŘEŠENÉ)
#3 26. 09. 2013 21:58 — Editoval Witiko (26. 09. 2013 22:32)
Re: Graf nezahrnuje spodní hemisféru
↑ Mihulik:
Ahoj,
ano, sudá odmocnina navrací dva kořeny: ![kopírovat do textarea $\sqrt[2n]{1} = \pm 1$](/mathtex/d6/d62f854d311a38f2fb3508ba424c4296.gif) .
.
Offline
#4 26. 09. 2013 22:02 — Editoval Mihulik (26. 09. 2013 22:12)
Re: Graf nezahrnuje spodní hemisféru
↑ Witiko:
Vždyť sudá odmocnina (jakožto reálná funkce) je nezáporná... A to je důvod, proč je to pouze polovina kulové plochy.
Ty dvě rovnice, které jsi uvedl, jsou sice ekvivalentní, ale jen za předpokladu, že 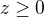 (a
(a 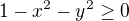 ).
).
Offline
#5 26. 09. 2013 22:13 — Editoval Witiko (26. 09. 2013 22:20)
Re: Graf nezahrnuje spodní hemisféru
↑ Mihulik:
Ale sudé odmocniny mají i záporný kořen. Pokud ![kopírovat do textarea $\sqrt[2n]{}$](/mathtex/ab/ab438699a5e2f9d726d98ec433fa56a6.gif) položíme jako relaci inverzní k
položíme jako relaci inverzní k 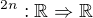 , pak
, pak 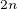 není injektivní, protože pro
není injektivní, protože pro 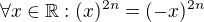 . Díky tomu není
. Díky tomu není ![kopírovat do textarea $\sqrt[2n]{}$](/mathtex/ab/ab438699a5e2f9d726d98ec433fa56a6.gif) reálnou funkcí, ale obecnou relací
reálnou funkcí, ale obecnou relací  , která pro
, která pro  navrací dvojici vzájemně opačných čísel.
navrací dvojici vzájemně opačných čísel.
Offline
#6 26. 09. 2013 22:21 — Editoval Mihulik (26. 09. 2013 22:39)
Re: Graf nezahrnuje spodní hemisféru
Ale mi přece nemluvíme o inverzní relaci k binární relaci sudé mocniny na množině 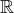 . Podíváme-li se na sudou mocninu, pak inverzní relace není zobrazení, to máš pravdu. Abychom mohli mluvit o zobrazení, potřebujeme uvážit restrikci definičního oboru relace na nezáporná čísla.
. Podíváme-li se na sudou mocninu, pak inverzní relace není zobrazení, to máš pravdu. Abychom mohli mluvit o zobrazení, potřebujeme uvážit restrikci definičního oboru relace na nezáporná čísla.
Nechť 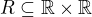 je relace sudé mocniny.
je relace sudé mocniny.
Máme 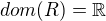 a
a 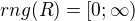 . Jak jsi zdůvodnil,
. Jak jsi zdůvodnil,  není funkce.
není funkce.
Ovšem uvážíme-li relaci ![kopírovat do textarea $S=\{[x;y]\in R;x\ge 0\}$](/mathtex/88/88940a2c0629f783c79227f6839549f2.gif) , pak
, pak 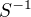 již funkce je a nazýváme ji (druhou) odmocninou. Samozřejmě jsme mohli vzít i jinou restrikci, ale tohle je to, co se implicitně předpokládá.
již funkce je a nazýváme ji (druhou) odmocninou. Samozřejmě jsme mohli vzít i jinou restrikci, ale tohle je to, co se implicitně předpokládá.
Offline
#7 26. 09. 2013 22:29 — Editoval Witiko (26. 09. 2013 22:46)
Re: Graf nezahrnuje spodní hemisféru
↑ Mihulik:
Ale to je potom solidní guláš. Když máš zadanou rovnici např.:  , tak ji řešíš následovně:
, tak ji řešíš následovně:
Zde tedy odmocninu zjevně chápeme jako obecnou relaci navracející dva kořeny. Kdy tedy na sudou odmocninu uvalujeme omezení na nezáporná čísla a kdy ne?
Offline
#8 26. 09. 2013 22:37 — Editoval Mihulik (26. 09. 2013 22:37)
Re: Graf nezahrnuje spodní hemisféru
↑ Witiko:
Ale to je přece něco jiného. Ty hledáš, nejsou-li daná nějaká omezení, všechna reálná čísla, jejichž kvadrát je roven 4. Tím, že "odmocníš", se právě omezíš jen na tu restrikci. Naštěstí zde je náprava jednoduchá, protože víme, že druhá mocnina je sudá. A tedy, je-li 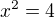 , pak nutně i
, pak nutně i  . Proto ta absolutní hodnota.
. Proto ta absolutní hodnota.
Offline
#9 26. 09. 2013 22:44
Re: Graf nezahrnuje spodní hemisféru
↑ Mihulik:
Vida, a já si myslel, že při odmocňování chceme vždy znát všechna reálná čísla, jejichž kvadrát je něčemu roven. V případě odmocniny jako reálné funkce (tvé 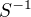 ) se tedy omezujeme na kladný kořen a pokud hledáme všechna reálná čísla, jejichž kvadrát je něčemu roven, použijeme bezejmennou
) se tedy omezujeme na kladný kořen a pokud hledáme všechna reálná čísla, jejichž kvadrát je něčemu roven, použijeme bezejmennou  , které jsem já dodnes pomýleně říkal odmocnina.
, které jsem já dodnes pomýleně říkal odmocnina.
Offline
#11 26. 09. 2013 23:38 — Editoval Witiko (26. 09. 2013 23:54)
Re: Graf nezahrnuje spodní hemisféru
↑ Mihulik:
Jen jsem neformálně přeformuloval to, co jsi tak pěkně formálně rozepsal v příspěvku #6. Díky! :-)
Offline
#18 27. 09. 2013 08:10 — Editoval LukasM (27. 09. 2013 08:25)
Re: Graf nezahrnuje spodní hemisféru
↑ Witiko:
Ano, navrací jen kladný kořen, a to je v našem případě právě ten problém. Ale my nejsme troubové a víme, že řešení existuje ještě jedno, a to má u sebe jen mínus navíc. Pokud víš, že 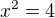 , co to znamená? Znamená to, že
, co to znamená? Znamená to, že 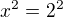 - tedy že se rovnají druhé mocniny nějakých dvou čísel. To znamená že jsou buď stejná, nebo opačná. Buď tedy platí
- tedy že se rovnají druhé mocniny nějakých dvou čísel. To znamená že jsou buď stejná, nebo opačná. Buď tedy platí  , nebo platí
, nebo platí 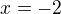 . Co tím pádem platí určitě je
. Co tím pádem platí určitě je 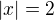 . Tak proč to tak nezapsat? Neříká to nic jiného. Když ale napíšu
. Tak proč to tak nezapsat? Neříká to nic jiného. Když ale napíšu  , přijdu o jedno řešení.
, přijdu o jedno řešení.
Zkrátka a dobře, 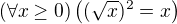 . Opačný případ ale tak jednoduchý není, a dá se psát
. Opačný případ ale tak jednoduchý není, a dá se psát 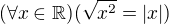 , tím umocněním tady totiž ztratím informaci o znaménku x. Platí to pro všechna reálná čísla - díky té mocnině mám pod odmocninou vždy kladné číslo. Ale to ještě neznamená, že původní x bylo taky kladné.
, tím umocněním tady totiž ztratím informaci o znaménku x. Platí to pro všechna reálná čísla - díky té mocnině mám pod odmocninou vždy kladné číslo. Ale to ještě neznamená, že původní x bylo taky kladné.
Edit: ještě to zkusím jinak. Ta aplikace odmocniny na rovnici 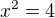 vytvoří rovnici
vytvoří rovnici 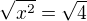 . Zbytek už není aplikace funkce, ale tvoje úpravy. Které když děláš dobře, skončíš s absolutní hodnotou.
. Zbytek už není aplikace funkce, ale tvoje úpravy. Které když děláš dobře, skončíš s absolutní hodnotou.
Offline
#20 27. 09. 2013 18:08
Re: Graf nezahrnuje spodní hemisféru
↑ Witiko:
Aha, tak to se bavíte o něčem úplně jiném než jsem myslel. Slovo relace jsem v zadání nikde neviděl.
Ale ať už se tu bude dít cokoli a ta formalizace dopadne jakkoli, troufám si tvrdit, že graf funkce v zadání  bude pořád popisovat jen horní polovinu koule. Tak nevím k čemu to tu má vést. Budu to radši jen sledovat.
bude pořád popisovat jen horní polovinu koule. Tak nevím k čemu to tu má vést. Budu to radši jen sledovat.
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Graf nezahrnuje spodní hemisféru (TOTO TÉMA JE VYŘEŠENÉ)

![kopírovat do textarea $\text{Výsledek: Grafem je horní polovina kulové plochy (leží v poloprostoru z } \ge \text{ 0), jejímž středem je [0, 0, 0] a poloměr je 1.}$](/mathtex/d8/d88912c301069e2e4402644b88588b74.gif)
 je přeci ekvivalentní
je přeci ekvivalentní  . Jedná se tedy o kouli celou.
. Jedná se tedy o kouli celou.
 ?:)
?:)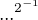 ? 4 se nám promítne na vzory 2 a -2. Princip je stejný a formálně čistý.
? 4 se nám promítne na vzory 2 a -2. Princip je stejný a formálně čistý. , tak výsledná rovnice je právě řešením aplikace relace
, tak výsledná rovnice je právě řešením aplikace relace 

 , tím dostaneme
, tím dostaneme 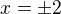 , ale to už nemá nic společnýho s tou odmocninou
, ale to už nemá nic společnýho s tou odmocninou formalizujeme.
formalizujeme.