Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 29. 09. 2013 11:47 — Editoval cutrongxoay (29. 09. 2013 12:48)
- cutrongxoay

- Příspěvky: 286
- Pozice: Student
- Reputace: 1
Rovnice tecny k dane kuzelosecce
Zdravim,
mam takove zadani ![kopírovat do textarea $M[1;-1]$](/mathtex/27/27b5d3ff3a077d45850b181a8b09be44.gif)
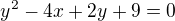
a ukolem je napsat rovnici tecny, ktere lze sestrojit z bodu M.
-------- -------- -------- -------- --------
Rovnici kuzelosecky jsem upravil do tvaru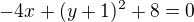
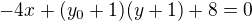
Problem je v tom, ze kdyz dosadim ten bod tak vyjdou jen cisla a ze je to rovno nule je blbost.
Jak mam prosim vas pokracovat dale ?
Offline
- (téma jako nevyřešené označil(a) jelena)
#2 29. 09. 2013 12:36 — Editoval jelena (29. 09. 2013 14:44)
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Rovnice tecny k dane kuzelosecce
Zdravím,
Ty předpokládáš, že bod M leží na kuželosečce (třeba překontrlovat a podle toho postupovat). Věřím, že po kontrole už problém s výpočtem nebudeš mít, jen pro seznámení s postupem od kolegů - hodně podrobně a kompletně tuto úlohu zpracovali na MatWiki. Kolegům děkuji.
Edit: opraveno "Kružnice" na "Kuželosečka".
Offline
#3 29. 09. 2013 13:23
Re: Rovnice tecny k dane kuzelosecce
↑ cutrongxoay:
Je to tečna k parabole z vnějšího bodu. Ten tvůj vztah nebude fungovat. Ten platí jen pro bod dotyku a stejně ho máš špatně.
Postup:
a) předpokládáme tečnu ve tvaru
Protože prochází bodem  , musí platit
, musí platit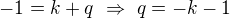
b) dosadíme  do rovnice kuželosečky
do rovnice kuželosečky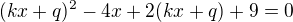
a roznásobíme
Měl bys dostat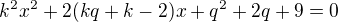
Tato kvadratická rovnice musí mít diskriminant roven nule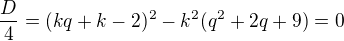
Opět roznásobíš a poupravuješ
c)
Měl bys dostat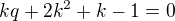
dosadíš za  a dopočítáš
a dopočítáš 
Pořádek je pro blbce, inteligent zvládá chaos!
Offline
#4 29. 09. 2013 13:44
- cutrongxoay

- Příspěvky: 286
- Pozice: Student
- Reputace: 1
Re: Rovnice tecny k dane kuzelosecce
↑ zdenek1:
" Ten platí jen pro bod dotyku"...a proc teda jde resit tim samym zpusobem tecnu pro kruznici i kdyz neznam zadne tecne body? U te paraboly se to prave snazim zjistit a prevod do stredoveho tvaru neni jeho postup reseni? 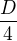 Tohle znamena co prosim? Vidim poprve.. Ja diskriminant chapu jako
Tohle znamena co prosim? Vidim poprve.. Ja diskriminant chapu jako 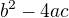
Offline
#5 29. 09. 2013 14:42
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Rovnice tecny k dane kuzelosecce
↑ zdenek1:
Zdravím a děkuji,
omlouvám se - v příspěvku 2 mám na mysli kuželosečku obecně (v odkazu na MatWiki jste to také tak zpracovali, jen poslední případ je speciálně kružnice). Opravím v příspěvku - ne kružnice, ale kuželosečka. ještě se podívám na MatWiki na postup pro "vzorec tečny" - viz dotaz kolegy.
↑ cutrongxoay:
kolega Zdeněk to také tak chápe, když budeš dosazovat do Tvého vzorce a, b, c ze zápisu kvadratické rovnice, co vznikla, tak se objeví násobek 4 u každého členu, tak tu 4 vytýká.
Offline
#6 29. 09. 2013 15:16 — Editoval vanok (29. 09. 2013 15:16)
Re: Rovnice tecny k dane kuzelosecce
Poznamka:
Toto vedeli stredoskolaci v mnohych europskych zemiach aspon do 70 rokov minuleho storocia.
Parabola rovnici  ma v bode
ma v bode  dotycnicu rovnici:
dotycnicu rovnici: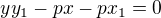
Od kedy to uz skoro nikto nevie?
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#7 29. 09. 2013 15:24
- cutrongxoay

- Příspěvky: 286
- Pozice: Student
- Reputace: 1
Re: Rovnice tecny k dane kuzelosecce
↑ vanok:
Zdravim,
my jsme teprve zacali u kruznice, ale s tim, ze jsem seminarnik, potrebuju vedet o neco vice, takze to berte jako samostudium. O jinych kuzeloseckach se prave chci dozvedet.
Offline
#8 29. 09. 2013 15:39
Re: Rovnice tecny k dane kuzelosecce
Ano, to je asi dost tazka uloha najst dobru literaturu na tu temu.
A po Sk ci Cz je to este komplikovanejsie.
Taka zaujimava tema je teorema od Dandelen-Guetelet. Velmi poucne!
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#9 29. 09. 2013 15:57
- cutrongxoay

- Příspěvky: 286
- Pozice: Student
- Reputace: 1
Re: Rovnice tecny k dane kuzelosecce
↑ vanok:
Tak prominte, ze jsem dyslektik...za to hold nemuzu.
Offline
#10 29. 09. 2013 16:09
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Rovnice tecny k dane kuzelosecce
↑ cutrongxoay:
prosím, nevytvářej zbytečné problémy. To se vyjasní. Kolega vanok má neskutečný přehled, doporučuji pomalu postudovat. Z čeho, prosím, studuješ? Děkuji.
↑ vanok:
Zdravím,
nemyslím, že by kolega měl problém s materiály (případně to upřesní, uvede, z čeho studuje, doplníme). V ČR nejlepší učebnice je sada pro Gymnázia a Přehled SŠ matematiky od Poláka - věřím, že v semináři bylo doporučeno.
Můj názor - pokud rozumím principu vzájemné polohy kuželosečky a přímky (jeden společný bod), potom cesta kolegy ↑ zdenek1: (a více nás to používá) prokazuje, že problému rozumím.
Více mechanické je použití hotového vzorce - předpokládám, že se využívá vlastnost poláry. Je tak?
Další cesta je využití diferenciálního počtu - kolega pravděpodobně ještě k tomu nedošel, ale časem určitě metody shrne. Je to obdobné téma debaty, jak jsme řešili - že je více metod.
Můžeme se takto dívat? Děkuji.
Offline
#11 29. 09. 2013 17:55 — Editoval vanok (29. 09. 2013 17:57)
Re: Rovnice tecny k dane kuzelosecce
↑ jelena:
Pozdravujem,
Tie materialy co radis kolegovy nepoznam, ale iste ide o dobre knihy.
V dobe o ktorej pisem, v mojom prispevku: zaklady o kuzelozeckach sa ucili bez diferencianelho poctu, a pouzivali sa potom metody blizke prispevku kolegu ↑ zdenek1: ... Ci su na to zvyknuty dnes stredoskolaci, to neviem posudit. A pochopitelne specialne, na polozeny problem, je viac moznosti na jeho riesenie.
Problem co som radil kolegovy, na konci mohol prispevku je bonus o kuzelozeckach a oplati sa kazdemu pozriet o co ide.
Peknu nedelu.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#12 30. 09. 2013 11:25 — Editoval Cheop (30. 09. 2013 12:21)
- Cheop


- Místo: okres Svitavy
- Příspěvky: 8209
- Škola: PEF VŠZ Brno (1979)
- Pozice: důchodce
- Reputace: 366
Re: Rovnice tecny k dane kuzelosecce
↑ cutrongxoay:
Máme-li parabolu ve tvaru: kde m, n jsou souřadnice vrcholu paraboly
kde m, n jsou souřadnice vrcholu paraboly
a vnější bod paraboly o souřadnicích x_0; y_0,kterým má procházet tečna, potom
pro přímku, která prochází tečnými body platí: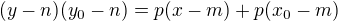
Průsečík této přímky a paraboly nám dá souřadnice tečných bodů.
Tečna je potom přímka,která prochází vnějším bodem a tečným bodem
Nikdo není dokonalý
Offline
#13 30. 09. 2013 11:34
Re: Rovnice tecny k dane kuzelosecce
Ahoj ↑ Cheop:,
Vidim, ze pouzivas pristup ako ten, co som navrhol.
Uci sa to este ?
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#15 01. 10. 2013 10:12
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Rovnice tecny k dane kuzelosecce
Zdravím, kolegové,
doplním jak bylo u nás na Východě, SŠ jsem končila v roce 1980, měli jsme 8 let ZŠ s výstupní zkouškou + 2 roky SŠ s maturitní zkouškou (celkem je to 10 let všeobecně vzdělávací střední škola bez přestupu na jinou).
Analytiku jsme v tomto programu neměli, až na VŠ v 1. ročníku, jen základy vektorů byly zařazeny na SŠ do geometrie (samostatný předmět). Ještě jsme měli předmět "Algebra a základy analýzy". Tipuji, že zde jsme mohli mít i kuželosečky jako funkce a vzájemné polohy s přímkou jako průsečík funkcí (tedy 1. metoda kolegy Zdeňka). Potom na VŠ jsme měli vzorec pro tečnu kuželosečky ve tvaru jak uvádí kolega Cheop, ale pro bod na kuželosečce.
V Eliášovi pro VŠ jsem takové vzorce, jak povídáte, našla (i v Bartsch). Všimnete si komentáře v bodu 6 - zda zde nevzniká nedorozumění, že vzorec se téměř výhradně používá pro bod na kuželosečce. Také si všimnete reakce kolegy Zdeňka (a moji), že vylučujeme použití vzorce pro bod mimo kuželosečku. Teď by bylo dobré, aby kolega ↑ cutrongxoay: doplnil jak je to se vzorcem u nich.
Prošla jsem Poláka z roku 1972, tam o poláře jsem nic nenašla, z elektronické učebnice pana Krynického - u kružnice poláru a postup běžně používá, ale u paraboly zamítá (viz př. 5).
Na MatWiki od kolegy Cheopa je to 2. postup. Jelikož na tento postup se hodně odkazujeme, možna by stalo za to přidat komentář o vlastnosti, která se využívá (o poláře) a také přidat postup nebo komentář i pro jinou kuželosečku, než kružnici. Nevím tedy, kde došlo k "vynechání informace".
Ale výzkum jsem včera večer provedla (proloženo dohledem nad slohovkou, referátem a přepisem Čtenářského deníku :-)) Nevíte, prosím, kdo je to ten OcDr. od kterého mám Eliase? Děkuji.
Offline
#16 01. 10. 2013 16:24
Re: Rovnice tecny k dane kuzelosecce
↑ jelena:
Pozdravujem,
Zaujimavy prispevok a popisuje ako si sa dostala ku kuzeloseckam.
Dufam ze si mala cas a si nieco nasla o teoreme co som naznacil tu ↑ vanok: uplne na konci.
Ide (o pekny dokaz) o suvis slova kuzelosecka a z tym co sa uci ( ucilo?) na skolach.
Akoze ide o zaujimavu temu... Otvaram preto novu diskuziu na temu:co viete o kuzelozeckach?
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#17 01. 10. 2013 22:40 — Editoval jelena (01. 10. 2013 23:38)
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Rovnice tecny k dane kuzelosecce
↑ vanok:
Zdravím,
ano, děkuji, přiznám se, že větu jsem neznala - našla jsem po Tvém uvedení tento materiál. I když náš kolega Peta8 je skeptický vůči diplomkám v rámci didaktik, věřím, že toto je nejlepší prostředí, kde mohou vznikat.
O kuželosečkách se zkusím rozvzpomenout, ale už se mi to dost míchá - co bylo na škole a co jsem se přiučila během časů, co jsem doučovala.
Ještě bych se rada zeptala kolegy Zdeňka, jako zkušeného metodika, jak se stalo, že tato metoda, kterou diskutujeme, je neřeknu, že vyloučena, ale silně zastíněna? Vždyť se ukazuje, že je více pohodlná v použití - je tak? Vzpomínám (zkusím i najít), že jsme upravovali výraz, co nám vznik metodou  a bylo to trápení.
a bylo to trápení.
Edit: trápení bylo moje, kolega Zdeněk problém neměl :-)
Offline
#18 02. 10. 2013 08:26 — Editoval Cheop (02. 10. 2013 14:59)
- Cheop


- Místo: okres Svitavy
- Příspěvky: 8209
- Škola: PEF VŠZ Brno (1979)
- Pozice: důchodce
- Reputace: 366
Re: Rovnice tecny k dane kuzelosecce
↑ jelena:
Zdravím:-)
Tak abychom to uzavřeli.
Rovnice tečen ke kuželosečkám z vnějšího bodu kuželosečky pomocí poláry.
Kružnice
Mějme:
1) kružnici ve tvaru 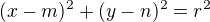 a vnější bod
a vnější bod ![kopírovat do textarea $X[x_0;\,y_0]$](/mathtex/e2/e23bb2a7af6acc1abebc35bbe8fdabf6.gif) kde m; n jsou souřadnice středu kružnice
kde m; n jsou souřadnice středu kružnice
2) Pro poláru tj. přímku, která prochází tečnými body platí: 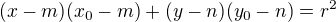
3) Průsečíky poláry s kružnicí nám určí souřadnice tečných bodů T
4) Tečna je potom přímka procházející bodem X a bodem T (přímka určená dvěma body)
Elipsa
1) Elipsa ve tvaru  a vnější bod
a vnější bod ![kopírovat do textarea $X[x_0;\,y_0]$](/mathtex/e2/e23bb2a7af6acc1abebc35bbe8fdabf6.gif) kde m; n jsou souřadnice středu elipsy
kde m; n jsou souřadnice středu elipsy
2) Pro poláru platí: 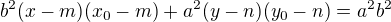
3) Průsečíky poláry s elipsou nám určí souřadnice tečných bodů T
4) Tečna je potom přímka procházející bodem X a bodem T (přímka určená dvěma body)
Hyperbola
1) Hyperbola ve tvaru  a vnější bod
a vnější bod ![kopírovat do textarea $X[x_0;\,y_0]$](/mathtex/e2/e23bb2a7af6acc1abebc35bbe8fdabf6.gif) kde m; n jsou souřadnice středu hyperboly
kde m; n jsou souřadnice středu hyperboly
2) Pro poláru platí: 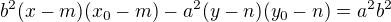
3) Průsečíky poláry s hyperbolou nám určí souřadnice tečných bodů T
4) Tečna je potom přímka procházející bodem X a bodem T (přímka určená dvěma body)
Parabola
1) Parabola ve tvaru  a vnější bod
a vnější bod ![kopírovat do textarea $X[x_0;\,y_0]$](/mathtex/e2/e23bb2a7af6acc1abebc35bbe8fdabf6.gif) kde m; n jsou souřadnice vrcholu paraboly
kde m; n jsou souřadnice vrcholu paraboly
2) Pro poláru platí: 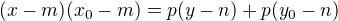
3) Průsečíky poláry s parabolou nám určí souřadnice tečných bodů T
4) Tečna je potom přímka procházející bodem X a bodem T (přímka určená dvěma body)
Nikdo není dokonalý
Offline
#19 02. 10. 2013 09:38
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Rovnice tecny k dane kuzelosecce
↑ Cheop:
Zdravím a obdiv :-) Ještě se to musí propašovat na MatWiki.
Vtip je v tom, že samotný tvar rovnice tečny je stejný jak pro bod na kuželosečce (a jak běžně používáme), tak i mimo kuželosečku - ale smysl použitého bodu je jiný a pro poláru ještě musí být další krok. Tedy se to dá pěkně standardizovat. Tak nevím, proč se nestandardizovalo - viz můj ↑ dotaz:?
Offline
#20 02. 10. 2013 10:50
Re: Rovnice tecny k dane kuzelosecce
Ahoj ↑ Cheop:,
Mozes upresnit co presne pre teba znamena pojem polara.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#21 02. 10. 2013 11:04
- Cheop


- Místo: okres Svitavy
- Příspěvky: 8209
- Škola: PEF VŠZ Brno (1979)
- Pozice: důchodce
- Reputace: 366
Re: Rovnice tecny k dane kuzelosecce
↑ vanok:
Definice
Přímka daná rovnicí 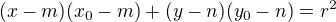 se nazývá polára bodu
se nazývá polára bodu ![kopírovat do textarea $X[x_0; y_0]$](/mathtex/f9/f9cbb0e5a6311649275399e6a5434d71.gif) vzhledem ke kružnici se středem
vzhledem ke kružnici se středem![kopírovat do textarea $ S[m; n]$](/mathtex/c1/c1c4d2b71dab5ea03526f7f8f5433d08.gif) a poloměrem r.
a poloměrem r.
Věta
Polára bodu ![kopírovat do textarea $X[x_0; y_0]$](/mathtex/f9/f9cbb0e5a6311649275399e6a5434d71.gif) vzhledem ke kružnici k se středem
vzhledem ke kružnici k se středem ![kopírovat do textarea $S[m; n]$](/mathtex/f1/f1792539c5b02a8ffae3ea85c2e9ca96.gif) a poloměrem r obsahuje body dotyku tečen kružnice k, procházejících bodem X.
a poloměrem r obsahuje body dotyku tečen kružnice k, procházejících bodem X.
Nikdo není dokonalý
Offline
#22 02. 10. 2013 11:51 — Editoval vanok (02. 10. 2013 13:38)
Re: Rovnice tecny k dane kuzelosecce
↑ Cheop:
Pozdravujem,
Podla mna treba robit suvis z harmonickym pomerom, ktory to umoznuje presne definovat. (cf. Projektivne kuzelosecky)
Cize sa mi zda, ze ide iba o pozostatok z dost ( velmi?) starych programov, pravdepodobne z 30 tych rokov minuleho storocia... a vtedy geometria bola pre vela ziakov az trapenie. Ale to mi mozes ty lepsie upresnit, ako sa vyvijali v Cz, Sk programy stredoskolskej matematiky.
A tiez by ma zaujimalo kedy sa prestala ucit kruhova inverzia?
Edit: na webe sa da najst, ze tie rovnice co volas polary, su zname skor pod menom zvojenie premennych kruznice, elipsy, hyperboly, paraboly... v danom bode.(pouzivane dost vela autormy ako aj mnemotechnicky prostriedok za zapametanie vysledkov, ktore dali do tej formy).
No vsak taky vysledok treba dokazat pre kazdu kuzelosecku.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#24 02. 10. 2013 13:52 — Editoval vanok (02. 10. 2013 13:54)
Re: Rovnice tecny k dane kuzelosecce
↑ Cheop:,
Ano napriklad, to je dobre riesenie... a mudrejsie podla dnesnych programov strednej skoly.
Ale tak ci tak, tvoja presentacia je pekne redigovanie viet o kuzeloseckach, uzitocnych pre stredoskolakov.
A co si ty mohol zistit o vyvoji skolskych programov?
Vyssie ↑ vanok: som do editoval co som nasiel o tom na webe.
Inac otvoril som vlakno o kuzeloseckach, mozno ta to zaujme.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#25 03. 10. 2013 10:56
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Rovnice tecny k dane kuzelosecce
↑ Cheop:, ↑ vanok:
Zdravím,
dívala jsem se na katedru didaktiky - materiály (2. odkaz není funkční) + seznam literatury k předmětu, také je zajímavé se podívat na str. matematických seminářů. To je pro přehled aktuálního stavu výuky (ale podrobně neznám, měli bychom někoho z kolegů oslovit, kdo je tomu blíž).
Hodně materiálů je také v digitální knihovně a jen pro zpestření - ze slovníků - karta názvosloví. No bohužel, kde vzít čas na podrobnější čtení (zejména, když osobně čtu raději něco jiného, než matematiku) :-)
Offline