Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 09. 10. 2013 20:55
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: limita
Zdravím,
už je pěkná úprava a styl, děkuji, jen nedávej své úlohy do "Zajímavých", ale do školních sekcí podle stupně školy, co studuješ (toto může být SŠ - přesouvám).
Pomůže v jmenovateli vytknout  a celý zlomek rozšířit tak, aby v čitateli vznikl vzorec
a celý zlomek rozšířit tak, aby v čitateli vznikl vzorec 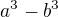 Odkaz.
Odkaz.
Offline
#4 09. 10. 2013 23:01
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: limita
↑ winner123:
předpokládám, že x ve jmenovateli se podařilo vytknout. Abys představil rozšíření, tak máme zlomek  a potřebujeme pomocí vzorce v odkazu rozšiřovat do
a potřebujeme pomocí vzorce v odkazu rozšiřovat do  , přičemž
, přičemž ![kopírovat do textarea $a=\sqrt[3]{27+x}$](/mathtex/33/331503c8679c15d89e7950666dda6c96.gif)
![kopírovat do textarea $b=\sqrt[3]{27-x}$](/mathtex/9c/9cbfece21b5d745ebb6e966a46db3e8c.gif)
Offline
#7 09. 10. 2013 23:38 — Editoval gadgetka (09. 10. 2013 23:40)
Re: limita
Musíš ten čitatel pěkně postupně roznásobit... :D...V čitateli zbyde 2x, zkrátí se s x ve jmenovateli a pak do té zbylé "obludy" ve jmenovateli dosadíš nulu a vyjde  ... a omlouvám se, že jsem se k tomu dostala až teď.
... a omlouvám se, že jsem se k tomu dostala až teď.
Nejsem učitelka, proto matematiku neučím, ale přímo ji řeším...
Offline
#8 10. 10. 2013 19:26
- Eratosthenes
- Příspěvky: 2764
- Reputace: 136
Re: limita
↑ winner123:
Ahoj,
probírali jste už l'Hospitalovo pravidlo? To by bylo podstatně jednodušší.
Budoucnost patří aluminiu.
Offline
#9 11. 10. 2013 10:14
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: limita
↑ Eratosthenes:
Zdravím a děkuji,
jednodušší by to bylo, ale to je takový místní folklor - za hodně starých času se zde prosadila výzva (snad hlavním autorem byl kolega Marian) "Dokaž, že to jde pomocí nástrojů ZŠ" (nejen u limit, ale u limit to šlo tak daleko, že kolega Ondřej při zpracování svého Rychlokurzu l´Hospital zcela vynechal a doplňoval až kolega Jarrro.
Určitě víš, že ten ZŠ vzorec se musí procvičit a potom již není obtížné část  zapisovat automaticky rovnou a "donásobenou část" si jasně představit. Hodí se například v zadáních hodně vysokých n v odmocninách a užití vzorce.
zapisovat automaticky rovnou a "donásobenou část" si jasně představit. Hodí se například v zadáních hodně vysokých n v odmocninách a užití vzorce.
Offline
![kopírovat do textarea $lim x->0 \frac{{\sqrt[3]{27+x}-\sqrt[3]{27-x}}}{x+2\sqrt[3]{x^{4}}}$](/mathtex/eb/ebde86415070131210a5625590029d9a.gif)

![kopírovat do textarea $\lim_{x\to0}\frac{{\sqrt[3]{27+x}-\sqrt[3]{27-x}}}{x+2\cdot\sqrt[3]{x^{4}}}$](/mathtex/3f/3ffaba20d3d2a02c97e93f4178f66785.gif)
![kopírovat do textarea $x+2\sqrt[3]{x^4}=x+2x\sqrt[3]{x}=x(1+2\sqrt[3]{x})$](/mathtex/92/923df76dda5345636576c584a5fbff88.gif)
![kopírovat do textarea $\lim_{x\to0}{\frac{\sqrt[3]{27+x}-\sqrt[3]{27-x}}{x(1+2\sqrt[3]{x})}}\cdot \frac{\sqrt[3]{(27+x)^2}+\sqrt[3]{(27+x)(27-x)}+\sqrt[3]{(27-x)^2}}{\sqrt[3]{(27+x)^2}+\sqrt[3]{(27+x)(27-x)}+\sqrt[3]{(27-x)^2}}$](/mathtex/ab/ab28e969ecf7f501879aa457ee5a5fc4.gif)