Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 04. 10. 2013 18:46
Pohyb kuličky
Ahoj, mám problém s jedním příkladem.
Mám určeno, že ve vagonu u jeho přední stěny je položená kulička. Vagon se rozjede rovnoměrně zrychleným pohybem a kulička se za čas t dostane k zadní stěně vagonu, neodrazí se a zůstane na místě. Mám určit zrychlení vagonu a dráhu ujetou vagonem během pohybu kuličky, když znám vzdálenost mezi přední a zadní stěnou vagonu, čas t za který se kulička dostane k zadní stěně vagonu a moment setrvačnosti kuličky.
Díky za pomoc.
Offline
- (téma jako vyřešené označil(a) Olínečka)
#2 05. 10. 2013 09:22 Příspěvek uživatele pietro byl skryt uživatelem pietro. Důvod: balast
#3 05. 10. 2013 10:12
Re: Pohyb kuličky
↑ Olínečka:
Tak já zkusím fyziku.
Na kuličku působí v soustavě spojené s vagónem inerciální síla  (a_v - zrychlení vagónu)
(a_v - zrychlení vagónu)
Dále na kuličku bude působit síla tření. Takže pohybové rovnice jsou (a_k - zrychlení kuličky) (za předpokladu, že se kulička valí bez prokluzování)
(za předpokladu, že se kulička valí bez prokluzování)
Z druhé rovnice vyjádříme 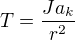 a dosadíme do první rovnice. Také využijeme vztah pro moment setrvačnosti koule
a dosadíme do první rovnice. Také využijeme vztah pro moment setrvačnosti koule  a dostaneme
a dostaneme
Pokrátíme a máme
Protože zrychlení kuličky můžeme spočítat z kinematických údajů
je 
a (dráha vagónu)
(dráha vagónu)
Pořádek je pro blbce, inteligent zvládá chaos!
Offline
#4 05. 10. 2013 11:39
#6 05. 10. 2013 21:03
- KennyMcCormick
- Příspěvky: 1677
- Reputace: 49
Re: Pohyb kuličky
Ve Zdeňkově řešení je  třecí síla a
třecí síla a  poloměr kuličky.
poloměr kuličky.
Even if you take the best course of action, the universe is still allowed to say "So what?" and kill you.
Offline
#9 07. 10. 2013 22:56
- KennyMcCormick
- Příspěvky: 1677
- Reputace: 49
Re: Pohyb kuličky
Úhlové zrychlení kuličky.
Even if you take the best course of action, the universe is still allowed to say "So what?" and kill you.
Offline
#11 08. 10. 2013 20:25 — Editoval pietro (08. 10. 2013 20:59) Příspěvek uživatele pietro byl skryt uživatelem pietro. Důvod: už mi to doklaplo
#12 08. 10. 2013 22:13 — Editoval KennyMcCormick (08. 10. 2013 22:34)
- KennyMcCormick
- Příspěvky: 1677
- Reputace: 49
Re: Pohyb kuličky
↑ Olínečka:
Co přesně na tom nechápeš?
Even if you take the best course of action, the universe is still allowed to say "So what?" and kill you.
Offline
#13 09. 10. 2013 12:57
Re: Pohyb kuličky
↑ Olínečka: Ahoj, dá sa to načrtnúť aj pomocou tohoto
http://fyzikalniolympiada.cz/texty/ulohy2.pdf
Příklad 9 – jojo
Tvoja úloha je analogická, s tým rozdielom, že pohyb sa deje nie v zvislom smere(jojo),
ale vo vodorovnom. Vlak ťahá + roztáča guličku.
Offline
#15 10. 10. 2013 03:06
- KennyMcCormick
- Příspěvky: 1677
- Reputace: 49
Re: Pohyb kuličky
Ne.
Even if you take the best course of action, the universe is still allowed to say "So what?" and kill you.
Offline
#16 10. 10. 2013 11:09
Re: Pohyb kuličky
↑ Olínečka:Ahoj, v príspevku 3 je stanovená úsporná, ale pevná a jednoznačná kostra riešenia.
Nauč sa prosím naspamäť Zdeňkove riešenie a uvidíš ako sa Ti polepší fyzikálny rozhľad. Úprimne.
A predstav si, že rotácia vždy spotrebuje energiu a preto napr. rotujúce jojo pomalšie padá ako voľným pádom pustené nerotujúce. Tam je rozdiel F-T.
Držíme palce.
Offline
#17 12. 10. 2013 18:27
Re: Pohyb kuličky
Ahoj, k tomuhle příkladu jsem dostala další úkol. Ještě mám zjistit velikost rychlosti kuličky před nárazem vzhledem k Zemi a rychlost kuličky bezprostředně po nárazu vzhledem k Zemi.
Nedala by se ta rychlost před nárazem vypočítat podle vzorce kde ak je zrychlení kuličky?
kde ak je zrychlení kuličky?
A jak vypočítat tu rychlost vzhledem k zemi po nárazu?
Díky.
Offline
#18 13. 10. 2013 15:24 — Editoval KennyMcCormick (13. 10. 2013 15:29)
- KennyMcCormick
- Příspěvky: 1677
- Reputace: 49
Re: Pohyb kuličky
Olínečka napsal(a):
Nedala by se ta rychlost před nárazem vypočítat podle vzorce
kde ak je zrychlení kuličky?
Musíme odečíst rychlost vagónu.
A jak vypočítat tu rychlost vzhledem k zemi po nárazu?
Kulička vůči vagónu po nárazu zůstane na místě, její rychlost tedy bude stejná jako rychlost vagónu:
EDIT: Promiň, nepřečetl jsem si to pořádně.
Even if you take the best course of action, the universe is still allowed to say "So what?" and kill you.
Offline
#20 13. 10. 2013 15:30
- KennyMcCormick
- Příspěvky: 1677
- Reputace: 49
Re: Pohyb kuličky
EDIT:
Oprava.
Even if you take the best course of action, the universe is still allowed to say "So what?" and kill you.
Offline


 ? Díky.
? Díky.