Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#5 10. 10. 2013 20:28
Re: hromadné body množiny
Diki, ešte sem pridám príklad, viem že by sa to nemalo, ale ide o to aby som to pochopil, preto sa to viacej hodí do jedného topicu ... Verím, že sa kompetentný nenahnevajú :)
a)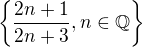
b)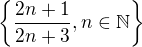
takze po a budu HB R* a po b HB=1 Ale uvahu, a zial bohu ani vypocet akosi neviem ...
Offline
#6 10. 10. 2013 23:30 — Editoval JohnPeca18 (10. 10. 2013 23:30)
- JohnPeca18

- Příspěvky: 651
- Škola: MFF UK
- Pozice: Absolvent 2014
- Reputace: 81
Re: hromadné body množiny
Ja bych skusil vypocet jako hint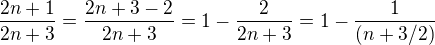
Takze tahle lomena funkce je posunuta funkce 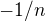 se "stredem" v
se "stredem" v ![kopírovat do textarea $[-3/2,1]$](/mathtex/94/943bdf89254df5c72e03d953be64292f.gif)
budes dal vedet?
Offline
#7 11. 10. 2013 01:01 — Editoval user (11. 10. 2013 01:46)
Re: hromadné body množiny
Ahoj,
příklad za a) mi přijde docela zajímavý, přidám svoje řešení, kde se pokusím ukázat, že je opravdu množina hromadných bodů R*
Offline
#8 11. 10. 2013 13:49
Re: hromadné body množiny
↑ JohnPeca18:
Dik tej vete sice nerozumiem, ale z toho výpočtu sa dá jednoducho urcit, že (1/(n+3/2)) ide k nule cize 1 bude bod v okolí ktorého sa vždy bude nachádzať aspoň 1 bod patriaci do tej množiny
Offline

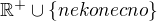
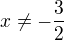 . Nejprve se podívám na funkci definovanou
. Nejprve se podívám na funkci definovanou 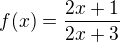 , tato funkce je spojitá a existuje k ní funkce inverzní. Jejím oborem hodnot je
, tato funkce je spojitá a existuje k ní funkce inverzní. Jejím oborem hodnot je  . Nechť je nyní
. Nechť je nyní  libovolné reálné číslo, ukážu, že se v jeho libovolném okolí nachází obraz nějakého racionálního čísla, což znamená, že je
libovolné reálné číslo, ukážu, že se v jeho libovolném okolí nachází obraz nějakého racionálního čísla, což znamená, že je 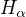 , vzorem tohoto okolí je opět nějaké okolí bodu
, vzorem tohoto okolí je opět nějaké okolí bodu  (vím že existuje inverzní funkce), nyní využiji faktu, že množina
(vím že existuje inverzní funkce), nyní využiji faktu, že množina 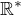 je množina hromadných bodů
je množina hromadných bodů  , to znamená, že existuje
, to znamená, že existuje 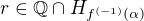 a tedy
a tedy  . To ale znamená, že množina hromadných bodů je opravdu
. To ale znamená, že množina hromadných bodů je opravdu  .
. nalézt vzor. Vzorem libovolného racionálního čísla
nalézt vzor. Vzorem libovolného racionálního čísla  je
je 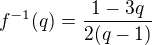 . Vzhledem k vlastnostem operací v
. Vzhledem k vlastnostem operací v