Matematické Fórum

pavell · 15. 10. 2013 22:20

Zdravim, prosim potřeboval bych tyto dva příklady, nevim jak na ně :-)
1) Spočtěte inverzní matici k matici $A^{-1}$

//forum.matweb.cz/upload3/img/2013-10/68392_2013-10-15%2B22.10.35.jpg
2) Spočtětedeterminant matice $A^{-1}$

pavell · 15. 10. 2013 22:23

pavell napsal(a):
Zdravim, prosim potřeboval bych tyto dva příklady, nevim jak na ně :-)
1) Spočtěte inverzní matici k matici $A^{-1}$

http://forum.matweb.cz/upload3/img/ … .10.35.jpg
první matice, je k prvnímu příkladu a druhá k druhýmu :-)
2) Spočtětedeterminant matice $A^{-1}$

kompik · 16. 10. 2013 08:55

pavell napsal(a):
Zdravim, prosim potřeboval bych tyto dva příklady, nevim jak na ně :-)
1) Spočtěte inverzní matici k matici $A^{-1}$

http://forum.matweb.cz/upload3/img/ … .10.35.jpg
2) Spočtětedeterminant matice $A^{-1}$

1) Jedna možnosť je dosadiť do Sarrusovho pravidla a upravovať.
Možno ľahší spôsob (resp. menšia pravdepodobnosť chyby) je využívať riadkové (a stĺpcové) operácie. Treba vedieť, ako tieto operácie menia determinant.

$\begin{vmatrix} 1 & 1 & -a \\ 2 &-1 & 3-a\\ 1 & a & -a \end{vmatrix}= \begin{vmatrix} 1 & 1 & -a \\ 0 &-3 & 3+a\\ 0 &a-1& 0 \end{vmatrix}= (1-a)\begin{vmatrix} 1 & 1 & -a \\ 0 & 1 & 0\\ 0 &-3 & 3+a \end{vmatrix}= (1-a)\begin{vmatrix} 1 & 1 & -a \\ 0 & 1 & 0\\ 0 & 0 & 3+a \end{vmatrix}=(1-a)(3+a)$

jelena · 16. 10. 2013 10:21

Zdravím v tématu,

pár laskavých Moderátorských poznámek ke kolegovi ↑ pavell: - nevkládej, prosím, do tématu více úloh + je dobré alespoň doplnit váš materiál, ze kterého studuješ, definici apod. pokud se vůbec nic nedaří viz pravidla. Také není dobré vkládat nečitelné scany - TeX používáš, pokud je problém se složitějším zápisem, je zde téma, kde se dá zeptat, nebo jsou vzory (pohledat téma, kde jsou matice a determinanty a okopírovat vzor), např. v polovině tématu je vložen zápis.
Pokud v tématu nikdo neodpovídal, lepší je editovat úvodní příspěvek, než přidávat nový - tak je téma považováno za odpovězené. Snad jsem nic nevynechala :-)

↑ kompik:

děkuji, jen drobnost - doporučení se vztahuje k výpočtu determinantu, ale ještě je požadavek sestavení inverzní matice, pro kterou toto doporučení je také vhodné - výpočet inverzní pomocí determinantu (z hlavního webu). Může být? Děkuji.

kompik · 16. 10. 2013 12:03

jelena napsal(a):
↑ kompik:

děkuji, jen drobnost - doporučení se vztahuje k výpočtu determinantu, ale ještě je požadavek sestavení inverzní matice, pro kterou toto doporučení je také vhodné - výpočet inverzní pomocí determinantu (z hlavního webu). Může být? Děkuji.

O inverznej matici som nepísal zatiaľ nič. Pokiaľ ide o výpočet determinantu matice 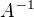$A^{-1}$ tak si stačí uvedomiť, že $\det A^{-1}\cdot \det A=1$ . (Na to sa dá prísť, keď vieme, čomu sa rovná determinant súčinu matíc a determinant jednotkovej matice.)
Pokiaľ chceme vyrátať inverznú maticu (takéto niečo je v tej druhej úlohe - tú som naschvál ignoroval, lebo jedna téma má byť jedna úloha), tak už bude treba urobiť aj niečo viac. A je to presne tak ako píše jelena - postup cez riadkové úpravy, taký ako v tom odkaze, by mohol zabrať. (Keďže sa tu vyskytuje parameter a, treba úpravy skúsiť robiť inteligentne; ak sa dá, tak sa vyhýbať zložitým výrazom s parametrom; keď už idem robiť nejaká úpravu, kde delím výrazom obsahujúcim parameter, mal by som si rozmyslieť, či nedelím nulou.)

jelena · 16. 10. 2013 14:04

↑ kompik:

děkuji, upozornění ohledně parametrů určitě přijdou vhod. Jinak - pokud zcela odmyslím úlohu 2), tak v názvu tématu je sice determinant, ale zadání k úloze 1) je

1) Spočtěte inverzní matici k matici $A^{-1}$

:-) což stačí zadanou matici A jen přepsat. No zkrátka autor tématu si musí více dát záležet na přípravě tématu.

Matematické Fórum

#1 15. 10. 2013 22:20

Determinant

#2 15. 10. 2013 22:23

Re: Determinant

pavell napsal(a):

#3 16. 10. 2013 08:55

Re: Determinant

pavell napsal(a):

#4 16. 10. 2013 10:21

Re: Determinant

#5 16. 10. 2013 12:03

Re: Determinant

jelena napsal(a):

#6 16. 10. 2013 14:04

Re: Determinant

Zápatí