Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 16. 10. 2013 19:50
Pravděpodobnost, tahaní koulí
Máme dvě urny: světlou, v níž jsou 2 modré a 2 červené koule,
a tmavou, v níž je 1 modrá a 3 červené koule. Nejprve si hodíme
kostkou: pokud padla šestka, vybereme si světlou urnu; jinak
vybereme tmavou. Z vybrané urny poté vytáhneme náhodně jednu kouli.
Jaká je pravděpodobnost, že na kostce padla šestka, byla-li vytažena
červená koule?
Jak to vypočítám?
díky
Offline
#2 16. 10. 2013 21:02 — Editoval user (16. 10. 2013 21:18)
Re: Pravděpodobnost, tahaní koulí
Ahoj,
jedná se o příklad, k jehož výpočtu je vhodné použít Bayesovu větu http://en.wikipedia.org/wiki/Bayes%27_t … ended_form
Offline
#7 17. 10. 2013 11:05
Re: Pravděpodobnost, tahaní koulí
↑ Domki:
Dobrý den, asi Vám jen učitel neřekl, že se jedná o Bayesův vzorec. Pokud se v tom ještě neorientujete, použiji (s dovolením) značení kolegy ↑ user: a trochu to rozvedu: - na kostce padne 6
- na kostce padne 6 - na kostce nepadne 6
- na kostce nepadne 6 - tedy, když se táhne z první urny = 2/4 = 1/2
- tedy, když se táhne z první urny = 2/4 = 1/2 - tedy, když se táhne z druhé urny = 3/4
- tedy, když se táhne z druhé urny = 3/4 - je vytažena červená (bez ohledu na to, co padlo na kostce):
- je vytažena červená (bez ohledu na to, co padlo na kostce):
S využitím Vámi uvedeného vzorce: ,
, 

 , je hledaná pravděpodobnost.
, je hledaná pravděpodobnost.
Když dosadíte, musí vyjít to, co vyšlo kolegovi ↑ user:.
Pokud se tedy nemýlím.
Offline
#8 17. 10. 2013 11:19
Re: Pravděpodobnost, tahaní koulí
Neodpustím si abych taky nenapsal svůj pohled na věc, podobný jako tady. Pravděpodobnost že padla 6 a vytáhnul jsem červenou je  (v té bedně je polovina koulí červených). Prst že padne 1-5 a vytáhnu červenou je
(v té bedně je polovina koulí červených). Prst že padne 1-5 a vytáhnu červenou je  . Žádný jiný způsob jak bych mohl vytáhnout červenou už není. Přitom vím, že červená padla, takže mně zajímá jaké procento tvoří ty šestkové tahy oproti všem kdy jsem vytáhl červenou. To je tedy
. Žádný jiný způsob jak bych mohl vytáhnout červenou už není. Přitom vím, že červená padla, takže mně zajímá jaké procento tvoří ty šestkové tahy oproti všem kdy jsem vytáhl červenou. To je tedy  . Hotovo. Samozřejmě postup je nakonec stejný jako při aplikace oněch vět, ale dá se na to přijít i hlavou. Tím neříkám že ty vzorce není třeba umět, ale je dobré vědět co vlastně počítám.
. Hotovo. Samozřejmě postup je nakonec stejný jako při aplikace oněch vět, ale dá se na to přijít i hlavou. Tím neříkám že ty vzorce není třeba umět, ale je dobré vědět co vlastně počítám.
Offline

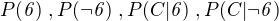
 . Nyní už to stačí dosadit.
. Nyní už to stačí dosadit.