Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Vyjadreni linearni fce ze zlomku linearnich fci s mocninou v citateli
#1 02. 11. 2013 17:10
Vyjadreni linearni fce ze zlomku linearnich fci s mocninou v citateli
Patrne se jedna o jednoduchy problem, ale ja ne to koukam jak jelen:
Mam dve linearni funkce promennych 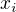 o koeficientech
o koeficientech 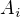 a
a 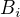 kde
kde 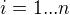
a upozornuji, ze n>30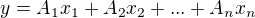
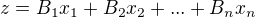
tyto funkce dosadim do nasledujiciho vztahu: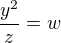
a nyni mam vyjadrit take  jako linearni funkci
jako linearni funkci 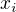 s koeficienty
s koeficienty 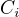 kde opet
kde opet 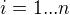
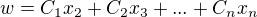
Otazka zni, jak vyjadrit koeficienty 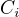 ?
?
Ja vubec nevidim, jak to udelat, mozna, ze se po me chce to ten vyraz ve zlomku nejakym zposobem linearizovat?
Diky za napady.
Offline
#2 02. 11. 2013 21:18
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Vyjadreni linearni fce ze zlomku linearnich fci s mocninou v citateli
Zdravím,
zkoušel jsi provést jen pro nenáročný zápis, např. jen pro 2 členy 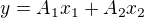
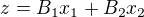 ?
?
Zkouším vyjádřit koeficienty pomocí dělení dvojčlenu dvojčlenem, ale pořád mi jeden člen přebývá, který nedokáží zapsat dle Tvé představy (tedy lineárně). Jak vznikl Tvůj dotaz? Děkuji.
Offline
#3 02. 11. 2013 21:32 — Editoval mrak (02. 11. 2013 21:35)
Re: Vyjadreni linearni fce ze zlomku linearnich fci s mocninou v citateli
↑ jelena:
Diky za odpoved,
Mno prave ze to nechapu ani s dvema členy, zkousel jsem na to jit podobne jako ty.
Problém je následující:
Ty linearni rovnice predstavují nejaky fyziklani model, ktery je popsany ve tvaru, kde koeficienty 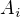 ,
, 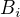 jsou zavisle na vstupech systemu, a
jsou zavisle na vstupech systemu, a 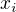 jsou konstanty urcujici chovani toho modelu. A ja potrebuju ty konstanty urcit, coz provadim fitovanim na ruzna namerena data (resim pres SVG dekopozici). Navic je explicitne dano, ze tato procedura je linearni problem, ktery se ma resit linearnimi metodami. Jenze jedna velicina, ktera se vyskytuje v souboru namernych date je
jsou konstanty urcujici chovani toho modelu. A ja potrebuju ty konstanty urcit, coz provadim fitovanim na ruzna namerena data (resim pres SVG dekopozici). Navic je explicitne dano, ze tato procedura je linearni problem, ktery se ma resit linearnimi metodami. Jenze jedna velicina, ktera se vyskytuje v souboru namernych date je  , ktere je urceno uvedenym vzorcem.
, ktere je urceno uvedenym vzorcem.
Offline
#4 02. 11. 2013 23:57
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Vyjadreni linearni fce ze zlomku linearnich fci s mocninou v citateli
↑ mrak:
děkuji, jen moje postřehy:
a) 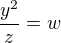 přepíšeme za předpokladu, že
přepíšeme za předpokladu, že 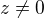 na
na 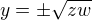 - za jaké podmínky
- za jaké podmínky 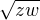 je lineární?
je lineární?
b) lineárně se podaří zapsat, když jsou odlišné koeficienty pouze u jedné neznámé 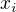 (a tuším, že má to za původ něco o kvadratických formách, čemu zas nerozumím, jen si to tak představuji) - vyjadřovalo by se hezky (příklad - pouze z má odlišný koeficient), ale asi Tvůj problém to neřeší.
(a tuším, že má to za původ něco o kvadratických formách, čemu zas nerozumím, jen si to tak představuji) - vyjadřovalo by se hezky (příklad - pouze z má odlišný koeficient), ale asi Tvůj problém to neřeší.
Tak snad ještě kolegové, děkuji.
Offline
#5 03. 11. 2013 00:32
Re: Vyjadreni linearni fce ze zlomku linearnich fci s mocninou v citateli
↑ jelena:
Ja nechci zabíhat do detailů, jelikož bych se v tom zamotal a nikdo by se v mem vykladu nevyznal, nicmene jeste trochu přibližím pozadí, možná je řešení trochu hlouběji:
Vychozi rovnice:
Funkce  z citatele je vyjadrena jako derivace p:
z citatele je vyjadrena jako derivace p:
tedy: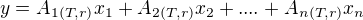
kde: 
Podobne je to s  v jmenovateli:
v jmenovateli: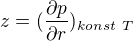
tedy: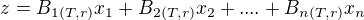
kde: 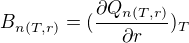
Pak  lze prepsat jako:
lze prepsat jako: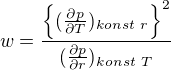
a ja hledam  ve tvaru:
ve tvaru: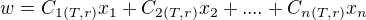
Tim je dano, ze linearní koeficinety na sobe zavisi, což by mohlo být k nečemu užitečné....
Kazdopadne dekuji za predchozí
Offline
#6 03. 11. 2013 00:57 — Editoval user (03. 11. 2013 01:06)
Re: Vyjadreni linearni fce ze zlomku linearnich fci s mocninou v citateli
Ahoj,
jestli jsem to dobře pochopil, tak máš funkce  a
a  jako lineární funkce n-proměnných a pak funkci
jako lineární funkce n-proměnných a pak funkci 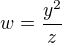 , po které chceš aby byla také lineární v těchto proměnných?
, po které chceš aby byla také lineární v těchto proměnných?
Obávám se, že obecně to lineární funkce nebude. Nicméně pokud problém pochází z fyziky a popisuje nějaký experiment, tak by mohla jít použít lineární aproximace v okolí nějakého bodu 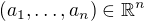 pomocí Taylorova rozvoje v okolí tohoto bodu.
pomocí Taylorova rozvoje v okolí tohoto bodu.
↑ jelena:
b) Taky se v tomto tématu příliš nevyznám, ale odhadl bych, že podmínka linearity  by šla ověřit právě tím Taylorem, kde by se ukázalo, že všechny vyšší derivace v rozvoji budou nulové.
by šla ověřit právě tím Taylorem, kde by se ukázalo, že všechny vyšší derivace v rozvoji budou nulové.
Offline
#7 03. 11. 2013 01:13 — Editoval mrak (03. 11. 2013 01:17)
Re: Vyjadreni linearni fce ze zlomku linearnich fci s mocninou v citateli
↑ user:
Ano asi to tak bude...linearizace je asi jedine reseni.
Ja nad tim badam, jelikož mam několik publikaci od nekolika autoru, ktere hovori o obecne linearite ulohy pro vetsinu promennych ( ,
, ,
, ...). V publikacich se sice zminuji, ze se v problemu mohou vyskytout i nelinearni promenne, ale nikdy nezmini promennou
...). V publikacich se sice zminuji, ze se v problemu mohou vyskytout i nelinearni promenne, ale nikdy nezmini promennou  . Dokonce mam publikace, kde promennou
. Dokonce mam publikace, kde promennou  evidentne pouzivaji a zadne problemy s nelinearitou ani naznakem nezminuji. Na druhou stranu, nikde neni vyslovene napsano, ze
evidentne pouzivaji a zadne problemy s nelinearitou ani naznakem nezminuji. Na druhou stranu, nikde neni vyslovene napsano, ze  je linearni vzhledem k
je linearni vzhledem k  .
.
Dekuji za rady
Offline
#9 03. 11. 2013 01:30
Re: Vyjadreni linearni fce ze zlomku linearnich fci s mocninou v citateli
↑ user:
vlaste tomu tak je,  jsou konstanty modelu.
jsou konstanty modelu.  ,
, jsou podminky, za kterych byla namerena velicina
jsou podminky, za kterych byla namerena velicina  .
.
Ja mam tedy namereno mnoho ruznych 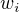 pro ruzne kombinace
pro ruzne kombinace 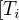 ,
,![kopírovat do textarea $r_{i}]$](/mathtex/53/53cdf1d012a2bc42e923ffc978b9176a.gif) a hledam
a hledam  koeficientu
koeficientu  funkce
funkce  , tak aby funkce
, tak aby funkce  (ktera obsahuje parcialni derivace
(ktera obsahuje parcialni derivace  ) sedela na namerene hodnoty
) sedela na namerene hodnoty 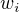 pro
pro 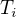 a
a 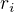 .
.
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Vyjadreni linearni fce ze zlomku linearnich fci s mocninou v citateli

 o které máš detailnější informace a zajímáš se o funkci
o které máš detailnější informace a zajímáš se o funkci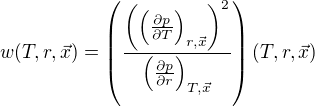 ,
,