Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Integrál - substituce - správný postup s výsledkem ?! (TOTO TÉMA JE VYŘEŠENÉ)
#2 20. 11. 2013 18:47
Re: Integrál - substituce - správný postup s výsledkem ?!
Myslím, že to máš špatně.
Chyba je v místě, kde jsi zintegroval výraz 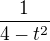 jako podíl logaritmů. Integrál součinů není součin integrálů :). Postupoval bych dále, vytknul bych 1/4 ze jmenovatele a upravil na výraz
jako podíl logaritmů. Integrál součinů není součin integrálů :). Postupoval bych dále, vytknul bych 1/4 ze jmenovatele a upravil na výraz 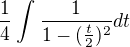 . Dále znovu substituuj s = t/2 a dostaneš vzorec pro arctg.
. Dále znovu substituuj s = t/2 a dostaneš vzorec pro arctg.
Offline
#3 20. 11. 2013 19:07
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Integrál - substituce - správný postup s výsledkem ?!
↑ hribayz:
Zdravím,
já bych řekla, že kolega to má dobře (zkus projít "kritické místo" přes parciální zlomky) - souhlasíš? Mám dojem, že na MENDELU v bílé knize je to ale vedeno jako tabulkový vzorec pod nějakým číslem V"něco" ↑ Fijojo: je tak? Děkuji.
Wolfram znám
MAW také? Ještě děkuji.
Offline
#4 20. 11. 2013 19:18
Re: Integrál - substituce - správný postup s výsledkem ?!
↑ hribayz:
Děkuji. Já tedy nemohu ve jmenovateli vytknout -1, aby se mi 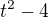 změnilo na
změnilo na 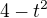 a tím pádem jsem měl
a tím pádem jsem měl 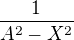 ?
?
-----------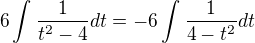
vzorec:
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Integrál - substituce - správný postup s výsledkem ?! (TOTO TÉMA JE VYŘEŠENÉ)

