Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Integrace metodou neurčitých koeficientů (TOTO TÉMA JE VYŘEŠENÉ)
#1 23. 11. 2013 01:02 — Editoval Fijojo (23. 11. 2013 01:07)
Integrace metodou neurčitých koeficientů
Dobrý den, potřeboval bych opět poradit. Tentokrát s metodou neurčitých koeficientů:
Jedná se mi o tyto tři příklady
A) 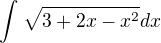
B) 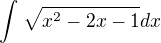
C) 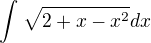
potřeboval bych každý příklad sestavit do této výchozí podoby, nějak mi to nejde.. (derivaci, úprava na rovnost polynomů atd. už doufám zvládnu sám).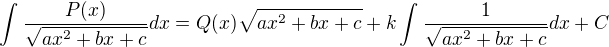
Zvládl jsem spočítat dva příklady: Takto jsem postupoval:
oba byly podobné:
např. jeden z nich: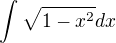
1. úprava: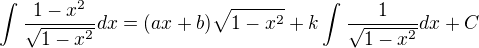
následně derivování: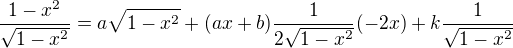
Pak jsem to vynásobil výrazem s odmocninou 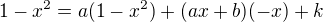
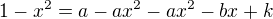
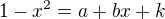
a provedl jsem úpravu na získání rovnosti polynomů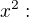
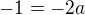

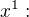
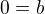
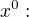
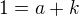

Dosadil jsem získané a/b/k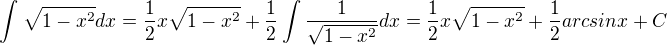
________________________________________
Snažil jsem se aplikovat tento přesný postup, ale nevyšlo mi to. Může mi prosím někdo s těmi příklady pomoct? Děkuji.
Offline
- (téma jako vyřešené označil(a) jelena)
#2 23. 11. 2013 10:55
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Integrace metodou neurčitých koeficientů
Zdravím,
tento postup pro 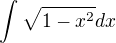 se ale podařil, potom bych předpokládala, že v dalších úlohách bude nějaký překlep při derivování nebo při hledání koeficientů. Ještě je možnost upravit výraz pod odmocninou na obdobný jako v podařené úloze
se ale podařil, potom bych předpokládala, že v dalších úlohách bude nějaký překlep při derivování nebo při hledání koeficientů. Ještě je možnost upravit výraz pod odmocninou na obdobný jako v podařené úloze 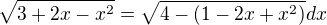 a zavést drobnou substituci. Podaří se dokončit? Další obdobně.
a zavést drobnou substituci. Podaří se dokončit? Další obdobně.
Ještě jsem tuto úlohu řešila na více způsobů (pomocí sbírky od Hlaváčka), snad také bude k prospěchu (i když u vás má být použita metoda dle vzorce V-..., že ano?). Tak (dle Ostrogradského) je zapracováno i v MAW.
Offline
#4 23. 11. 2013 13:51
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Integrace metodou neurčitých koeficientů
↑ Fijojo:
děkuji, hezké a přehledné. Řekla bych, že překlepy máš při derivování 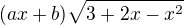 a to u 1. členu.
a to u 1. členu.
Potom
pro odstranění jmenovatele zlomku .../2 jsi celou rovnici vynásobil 2. Kde je to vidět v dalším řádku? Ale to opravuj až po opravě 1. derivování. Tak to ještě pro jistotu projdi, zda takových drobností není více.
Také se podívej na použití drobné substituce ↑ příspěvek 2: (bude daleko přehlednější)
Offline
Stránky: 1
- Hlavní strana
- » Vysoká škola: úvod do studia
- » Integrace metodou neurčitých koeficientů (TOTO TÉMA JE VYŘEŠENÉ)

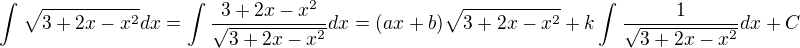
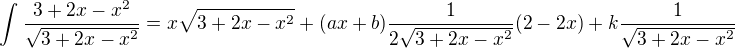
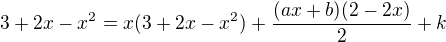
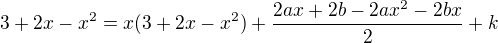
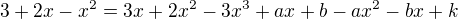
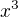 :
: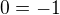
 :
: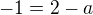 =>
=>
 :
: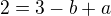 =>
=>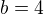
 :
: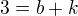 =>
=>
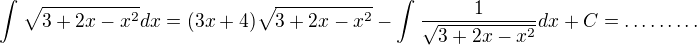
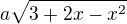 jsem to zderivoval jako
jsem to zderivoval jako 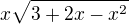 :))
:))