Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 19. 11. 2013 12:05
Re: Moivrevova věta
↑ Matiniela:
Dobrý den. Moivreova věta např tady:
http://cs.wikipedia.org/wiki/Moivreova_v%C4%9Bta
A s čím konkrétně je problém?
Pokud se tedy nemýlím.
Offline
#3 19. 11. 2013 12:22 Příspěvek uživatele Matiniela byl skryt uživatelem Matiniela.
#6 19. 11. 2013 16:01
Re: Moivrevova věta
Pokračoval bych použitím Moivrovy věty (viz. odkaz: http://cs.wikipedia.org/wiki/Moivreova_v%C4%9Bta) k výpočtu  a
a ![kopírovat do textarea $\sqrt[8]{c}$](/mathtex/88/88d4242826a913e8310022a89e396700.gif) .
.
Offline
#8 19. 11. 2013 16:43 — Editoval Jj (19. 11. 2013 16:54)
Re: Moivrevova věta
↑ Matiniela:
Řekl bych, že pokud sinus i cosinus je záporný, pak úhel leží
ve třetím kvadrantu, a
![kopírovat do textarea $[cos(4\pi/3)+isin(4\pi/3)]^8=cos(32\pi/3)+isin(32\pi/3)=$](/mathtex/3f/3fbed189b63ce7ac18b1703faef36d0c.gif)

Pokud se tedy nemýlím.
Offline
#10 19. 11. 2013 18:17 — Editoval Jj (19. 11. 2013 18:20)
Re: Moivrevova věta
↑ Matiniela:
To vyplývá z periodicity funicí sinus a kosinus (perioda =  ). Pro
). Pro  tyto funkce
tyto funkce
mají stejnou funkční hodnotu jako pro  . Hodnotu
. Hodnotu , tj. 5 celých period, je tudíž možno vypoustit a uvažovt jen hodnotu
, tj. 5 celých period, je tudíž možno vypoustit a uvažovt jen hodnotu 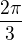 .
.
Pokud se tedy nemýlím.
Offline
#12 19. 11. 2013 19:20 — Editoval Jj (20. 11. 2013 19:15)
Re: Moivrevova věta
↑ Matiniela:
Osmá odmocnina (|c|=1):![kopírovat do textarea $[1*(cos(4\pi/3)+i\cdot sin(4\pi/3)]^\frac{1}{8}=\sqrt[8]{1}[ cos(\frac{4\pi/3+2k\pi}{8})+i\cdot sin(\frac{4\pi/3+2k\pi}{8})]=$](/mathtex/84/8488584899f8e341c50c547ddba7cb6c.gif)

Za 'k' dosazujte do vzorce postupně 0, 1, 2, .... 6, 7 a dostanete 8 osmých odmocnin
z čísla 'c' uvedeného v zadání.
Doplnění: pro zjednodušení ještě úprava vzorce (platí jen pro uvedenou osmou odmocninu!):
Pokud se tedy nemýlím.
Offline
#14 20. 11. 2013 19:00 — Editoval Jj (20. 11. 2013 19:00)
Re: Moivrevova věta
↑ Matiniela:
Výpočet pro k=0 je podle mě správně. Ano, každé z osmi takto získaných čísel je osmá odmocnina z 'c'. Každé z nich umocněné na osmou musí dát číslo c.
Pokud se tedy nemýlím.
Offline
#16 20. 11. 2013 19:14
Re: Moivrevova věta
↑ Matiniela:
Ano, pokračovat až do k=7, do řešení patří všechny výsledky.
Pokud se tedy nemýlím.
Offline
#18 20. 11. 2013 19:36
Re: Moivrevova věta
↑ Matiniela:
Řekl bych, že na tom už asi až tak nezáleží. Hlavně, abyste to dobře spočítal. Možná
by bylo dobré pro kontrolu výsledky ještě umocnit zpět na osmou a tím zkontrolovat
(vždy musíte opět dostat číslo c).
Pokud se tedy nemýlím.
Offline
#19 20. 11. 2013 19:40 — Editoval Matiniela (22. 11. 2013 18:27) Příspěvek uživatele Matiniela byl skryt uživatelem Matiniela.
#21 22. 11. 2013 20:20
Re: Moivrevova věta
U↑ Matiniela:
Řekl bych, že umocnění Vámi zveřejněného výsledku osmé odmocniny z čísla c vychází správně:
Vámi uvedená odmocnina čísla c:
Její zpětné umocnění na osmou:
 , což je původní číslo.
, což je původní číslo.
Pokud se tedy nemýlím.
Offline
#23 23. 11. 2013 14:54
Re: Moivrevova věta
↑ Matiniela:
Osmé odmocniny z
pro kontrolu viz tady: http://www.wolframalpha.com/input/?i=ta … k%3D0+to+7
(jen opisováním se to ještě nikdo nenaučil!).
Pokud se tedy nemýlím.
Offline





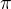 /3?
/3?
 c = a vypsat vsechny vysledky?
c = a vypsat vsechny vysledky?