Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 16. 11. 2013 17:21
- květinka fialová
- Příspěvky: 72
- Reputace: 0
Derivace
Mám zadané derivace![kopírovat do textarea $y=x+\sqrt{x}+\sqrt[3]{x}$](/mathtex/af/af8b905a174a9a26d5661988681c3936.gif)
![kopírovat do textarea $y=\frac{1}{x}+\frac{1}{\sqrt{x}}+\frac{1}{\sqrt[3]{x}}$](/mathtex/7c/7c0ce3b84f7fd8c8e48d9f2d9ce512fa.gif)
![kopírovat do textarea $y=\sqrt[3]{\frac{1-x}{1+x^{2}}+sin^3x*cos^2x}$](/mathtex/63/63c6c6d3c672d35111e28d440583dd1d.gif)

tak první příklad je ![kopírovat do textarea $y=1+\frac{1}{2\sqrt{x}}+\frac{1}{3\sqrt[3]{x^2}}$](/mathtex/49/49e581fc73a3c53c5c108399932f7492.gif)
druhý![kopírovat do textarea $y=-{x^2}+2\sqrt{x}+3\sqrt[3]{x^2}$](/mathtex/d9/d9d52405cc42360063952bf8827388e4.gif)
mohlo by být ?
Offline
#5 16. 11. 2013 17:58
Re: Derivace
Poznamka: funkcia derivacia funkcie y sa znaci y'
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#6 16. 11. 2013 18:13
- květinka fialová
- Příspěvky: 72
- Reputace: 0
Re: Derivace
a jak teda s tím
Vím,že je
je  což jde napsat i jako
což jde napsat i jako  no ale co pak s tím zlomkem ještě pod kterým ta odmocnina je
no ale co pak s tím zlomkem ještě pod kterým ta odmocnina je
nebo by to možna šlo ještě zapsat takto ne ? 
Offline
#8 16. 11. 2013 18:40
- květinka fialová
- Příspěvky: 72
- Reputace: 0
Re: Derivace
a to ![kopírovat do textarea $\frac{1}{\sqrt[3]{x}}$](/mathtex/1c/1c5cfcabeb277a84f4bef163aa816a63.gif) by podle tebe mělo vypadat takto
by podle tebe mělo vypadat takto 
Offline
#9 16. 11. 2013 18:45
- květinka fialová
- Příspěvky: 72
- Reputace: 0
Re: Derivace
takže zderivovaná funkce by měla vypadat takto 
Offline
#10 16. 11. 2013 18:54
#11 16. 11. 2013 19:21
- květinka fialová
- Příspěvky: 72
- Reputace: 0
Re: Derivace
jo to nějaký šotek ,to tam samozřejmě být nemá :)
Offline
#12 21. 11. 2013 17:21 — Editoval květinka fialová (21. 11. 2013 17:35)
- květinka fialová
- Příspěvky: 72
- Reputace: 0
Re: Derivace
![kopírovat do textarea $y=\sqrt[3]{\frac{1-x}{1+x^{2}}+sin^3x*cos^2x}$](/mathtex/63/63c6c6d3c672d35111e28d440583dd1d.gif)
postupuju tak že určim vnější funkci a do ní vložim nederivovanou vnitřní funkci a vynásobím to zderivovanou vnitřní funkci takže
a tohle mi vyplivnul wolfram 
Výsledek mi je k ničemu když nepochopím postup tak jestli byste mi zde mohli napsat jak se k tomu dostat ?
Offline
#14 23. 11. 2013 15:01
- květinka fialová
- Příspěvky: 72
- Reputace: 0
Re: Derivace
jo díky jen jsem byl zmatený z toho  pomohlo to no
pomohlo to no
tady bude zase vnitřní funkce odmocnina s tg a vnější mocnina
jakože vím,že odmocnina je něco na 1/2
tangens je 

ale nějak nevím jak to zkombinovat
Offline
#15 23. 11. 2013 22:34
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Derivace
↑ květinka fialová:
Zdravím, je silně nepřehledné všechno psát do jednoho tématu viz pravidla.
Pro poslední úlohu  prospěje použití návodů tohoto příspěvku, s největší pravděpodobnosti návodu č. 2, jehož zastáncem byl Marian.
prospěje použití návodů tohoto příspěvku, s největší pravděpodobnosti návodu č. 2, jehož zastáncem byl Marian.
Používáš vůbec MAW? Děkuji.
Offline

 to je jako
to je jako 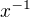 takže
takže 
 je
je 

![kopírovat do textarea $y=\sqrt[3]{\frac{1-x}{1+x^{2}}+sin^3(x)*cos^2(x)}$](/mathtex/3c/3cdedda0a9f813a4e5afe9008d4292f8.gif)





![kopírovat do textarea $(\sqrt[3]{\frac{1-x}{1+x^{2}}+sin^3(x)*cos^2(x)})'=$](/mathtex/b9/b9afc684d5948b4f922eb1c5689768d0.gif)

