Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 24. 11. 2013 17:52
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Kořeny funkce
Zdravím,
můžete používat grafický odhad umístění kořenů - přepisem na rovnost 2 funkcí?
Pokud ne, potom bych zkusila určit definiční obor funkce a pomocí vyšetření průběhu funkce naznačit extrémy. A dokončit, zda extrémy mají odlišná znaménka + možná něco jiného použitelného z průběhu. Jen takový námět (co je u vás v materiálech? děkuji).
Offline
#3 24. 11. 2013 18:47
Re: Kořeny funkce
Ahoj, díky moc za odpověď:o)
Veškeré materiály, co máme, se týkají už jen konkrétních metod na hledání kořenů v daném intervalu, jak onen interval odhadnout, o tom se už nikdo nezmiňuje.
Myslím, že můžeme použít i grafický odhad umístění kořenů, hlavní je, aby jsme to zdůvodnili i jinak než "tak dlouho jsem si zvětšovala tenhle kousek intervalu, až jsem tam ten kořen uviděla":o) Poradíš mi, prosím, jak to provést?
S tím průběhem funkce si taky pohraju, kouknu, co všechno se mi z vyšetřování podaří vytřískat:o)
Mockrát ti děkuju.
Offline
#4 24. 11. 2013 22:51
- Eratosthenes
- Příspěvky: 2936
- Reputace: 139
Re: Kořeny funkce
↑ Neth:
Ahoj,
ta funkce má podle mě kořeny jenom dva. Odhad najdeš nejlépe graficky podle rady ↑ jelena: - rozděl na hyperbolu a exponenciálu.
Budoucnost patří aluminiu.
Offline
#5 24. 11. 2013 23:42
Re: Kořeny funkce
Ahoj, díky.
Akorát jsem v tomto lehce omezená a potřebuju tohle popsat trochu více "prodebila". Rozdělím to na exponenciálu a hyperbolu a co pak?:o)
Maple a Wolphram a další mi tvrdí, že je reálný kořen i v okolí 2095 (když si v Maplu zvětším interval v týhle oblasti, opravdu tam na mě protnutí osy hledí). Je to chyba v nepřesných výpočtech či?
Offline
#6 25. 11. 2013 00:40
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Kořeny funkce
↑ Eratosthenes:
děkuji.
↑ Neth:
je to rovnost funkcí 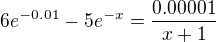 . Pomocí transformace základních grafů e^x a 1/x zakreslíš své funkce. Mně vychází, že exponenciála díky členu
. Pomocí transformace základních grafů e^x a 1/x zakreslíš své funkce. Mně vychází, že exponenciála díky členu 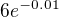 má přímku
má přímku  jako vodorovnou asymptotu, jinak je pod touto přímkou. Hyperbola má svislou asymptotu x=-1 ("posunuto" z 1. a 3. kvadrantu), tedy bych viděla jen 2 kořeny jako kolega ↑ Eratosthenes:. A asi ne moc daleko od -1, 0 a 1 (někde okolo). Co nabízí chytré stroje?
jako vodorovnou asymptotu, jinak je pod touto přímkou. Hyperbola má svislou asymptotu x=-1 ("posunuto" z 1. a 3. kvadrantu), tedy bych viděla jen 2 kořeny jako kolega ↑ Eratosthenes:. A asi ne moc daleko od -1, 0 a 1 (někde okolo). Co nabízí chytré stroje?
Ale nevím, zda by vyšetření extrému nebylo průkaznější.
Offline
#7 25. 11. 2013 10:46
Re: Kořeny funkce
Podle chytrých programů se kořeny nacházejí přibližně v okolí bodů -1.000001, -0.18 a 2095.26. Když jsem se snažila vyšetřit funkci a najít extrémy, tak se ukázalo, že skutečně něco by mělo být blízko -1 a 0, o 2095 ani ň, takže to opravdu bude mít dvě řešení.
Při grafickém hledání mě nechaly na holičkách inteligentní programy, ale spíš to je moje neschopnost s nimi pracovat:o) Bojuju dál.
Díky moc vám oběma, velmi mi pomáháte.
Offline
#8 25. 11. 2013 12:58
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Kořeny funkce
↑ Neth:
také děkujeme
o 2095 ani ň
když si představím grafy funkcí, tak nevidím žádný důvod, aby exponenciála přetnula hyperbolu v 3. bodu. Ještě můžeš přidat pro pěkné hodnoty x=-2, 0, 1 která z funkcí bude výš a která níž (pro x=-1 je jasná exponenciála, hyperbola by měly být "hluboko pod", jelikož zde má svou asymptotu).
Při grafickém hledání mě nechaly na holičkách inteligentní programy, ale spíš to je moje neschopnost s nimi pracovat:o) Bojuju dál.
:-) Přesunu do CAS a poprosím kolegy o vložení do "inteligentních programů". Děkuji.
Offline
#9 25. 11. 2013 15:33 — Editoval kaja.marik (25. 11. 2013 15:35)
- kaja.marik
- Veterán
- Příspěvky: 1915
- Reputace: 57
Re: Kořeny funkce
Neth napsal(a):
Maple a Wolphram a další mi tvrdí, že je reálný kořen i v okolí 2095 (když si v Maplu zvětším interval v týhle oblasti, opravdu tam na mě protnutí osy hledí). Je to chyba v nepřesných výpočtech či?
Me to wolframAlpha netvrdi: http://www.wolframalpha.com/input/?i=so … 28x%2B1%29
ani tam na me nic nehledi: http://www.wolframalpha.com/input/?i=pl … 95+to+2096
Offline