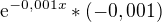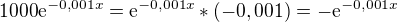Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 26. 11. 2013 10:47
Vyřešení monotonie
Zdravím, mám problém s určením monotonie dané funkce v množině M. Doufám, že mi někdo pomůže, protože já už si opravdu nevím rady :( . Zkoušela jsem to počítat pomocí definic, rostoucí a klesající funkce, ale vyšlo mi to pokažde jinak. Děkuji za pomoc 
Offline
#4 26. 11. 2013 11:10 — Editoval Bati (26. 11. 2013 11:11)
#6 26. 11. 2013 11:24
Re: Vyřešení monotonie
↑ Evulinka:
Jo, takže to ti celkem dá, že derivace je 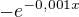 , což je vždycky...
, což je vždycky...
Offline
#7 26. 11. 2013 11:24 — Editoval Marian (26. 11. 2013 11:44)
Re: Vyřešení monotonie
↑ Evulinka:
Pokud se nepovoluje v zadání úlohy derivace, je možno použít pravidla platná pro monotonii funkce, která využívají monotonii vnější a vnitřní funkce. Současně je vhodné si uvědomit, že funkce  je pro
je pro  rostoucí (zvolíš-li konkrétně
rostoucí (zvolíš-li konkrétně  , jedná se de facto o náš případ, neboť platí dokonce
, jedná se de facto o náš případ, neboť platí dokonce  ).
).
Vnější funkce je  , která je rostoucí, tedy rostoucí je i její kladný násobek
, která je rostoucí, tedy rostoucí je i její kladný násobek 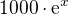 . Vnitřní funkce
. Vnitřní funkce 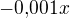 je klesající (lineární) funkce. Jak triviálně plyne z definice složené funkce, platí, že složení rostoucí s klesající je nutně klesající funkcí.
je klesající (lineární) funkce. Jak triviálně plyne z definice složené funkce, platí, že složení rostoucí s klesající je nutně klesající funkcí.
Derivace je druhá věc, kterou u této naprosto triviální ukázky lze také použít, ale vím, že zadání úlohy, kterou popisuješ, vyžaduje elementárnější diskusi, která je založena na vlastnostech skládání funkcí a monotonii funkcí elementárních. To samozřejmě nemohl tušit odpovídající člen tohoto fóra. Já jsem to tušit mohl, neboť mám s úlohou co do činění. Často (např. v triviálních ekonomických situacích) je použití pravidel o složené funkci ve vztahu k monotonii dílčích funkcí a výsledné funkce rychlejší.
;-)
Offline
#9 26. 11. 2013 11:41 — Editoval Bati (26. 11. 2013 11:42)
Re: Vyřešení monotonie
↑ Marian:
Sám jsem přemýšlel, kterou z variant doporučím, úlohu opravdu neznám. Rozhodl jsem se nakonec pro derivaci, protože téma je v sekci vysoká škola a postup nevyžaduje žádné další znalosti a přemýšlení:-) Co bych zvolil osobně je jiná věc.
Offline
#10 26. 11. 2013 11:42 — Editoval Marian (26. 11. 2013 11:42)
Re: Vyřešení monotonie
↑ Bati:
Rozumím tvému přístupu...
↑ Evulinka:
Ano, je klesající; ovšem záleží, který přístup je tvým pedagogem akceptován u této konkrétní úlohy.
Offline
#12 26. 11. 2013 12:00
Re: Vyřešení monotonie
↑ Evulinka:
To záleží ještě na tom, v jaké kapitole je uvedena úloha. V tomto případě to je před derivací, tedy použití derivace se bude obhajovat velmi nesnadně. Typ řešení úlohy je determinován i zařazením v příslušné kapitole.
Offline
#14 26. 11. 2013 12:49 — Editoval kaja.marik (26. 11. 2013 12:50)
- kaja.marik
- Veterán
- Příspěvky: 1915
- Reputace: 57
Re: Vyřešení monotonie
Evulinka napsal(a):
↑ Marian:
dobře tedy a mohl bys mi zaslat i výpočet tou druhou variantou ? :/
??? to uz se prece stalo v 11:24
Offline


 je rovno tomu samému, a se záporným znaménkem by to mělo být
je rovno tomu samému, a se záporným znaménkem by to mělo být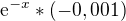 . Je to tak ??
. Je to tak ??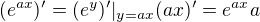 .
.