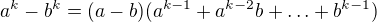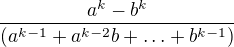Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#4 27. 11. 2013 00:32
Re: Limita
Ahoj,
jasný, to je pak to jediné složité v té limitě.
Pokusím se ještě jednou popsat jak se dobrat výsledku, protože, přiznám se bez mučení, se mi to nechce počítat do konce :)
Ve jmenovateli teď máme součet spousty (k) členů. n jde k nekonečnu, takže nás zajímá u každého členu, jaká je nejvyšší mocnicna enka a jaký je před ním koeficient. Nebude tedy záležet na tom, jaká je mocnina členů s +1 a jaká je mocnina členů s -1, protože n^k tyto nižší mocniny převáží. Máme tedy ve jmenovateli součet k členů, které se limitně chovají jako ![kopírovat do textarea $(\sqrt[k]{n^k})^{k-1}$](/mathtex/6d/6d5095e49ffcd2b52516576902fc8f34.gif) , celkově tedy limita dopadne jako
, celkově tedy limita dopadne jako ![kopírovat do textarea $\lim_{n\to\infty}\frac{n^{k-1}}{k\cdot(\sqrt[k]{n^k})^{k-1}}=\frac{1}{k}$](/mathtex/3e/3e6f5c610b29ca44604129c7fb75b33c.gif)
Korektně by se výpočet provedl přes převedení 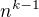 dovnitř odmocniny a zdůvodnění přes aritmetiku limit, že ve jmenovateli je k jedniček.
dovnitř odmocniny a zdůvodnění přes aritmetiku limit, že ve jmenovateli je k jedniček.
Offline
![kopírovat do textarea $\lim_{n\to \infty}n^{k-1}(\sqrt[k]{n^k +1} - \sqrt[k]{n^k -1})$](/mathtex/31/31e27592c706bb9abb68a66dec232ace.gif)