Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 08. 12. 2013 10:10 — Editoval PanTau (08. 12. 2013 10:23)
Největší objem z obdélníku..
Ahoj, mohl by mi prosím někdo poradit s následující úlohou? - Nejsem schopen na to přijít.
Z obdélníkového plechu o rozměrech 5×10 vytvoříme krabici tak, že v rozích vystřihneme stejné čtverce.Takto vytvořené krabice budou mít různé objemy.
Jaký bude největší objem V ?
Tohle mi má údajně pomoct :
----------------------------------------------------------------
Koukám že nejsem jediný co řeší tento problém :-)
http://forum.matweb.cz/viewtopic.php?id=67771
Jak píše paní jelena:
"Objem"=f(x), kde x je strana čtverce (následně tuto funkci vyšetřit na extrém, viz materiály)
Pokud se rovná V = abc
Ale jaký je nejmenší možný čtverec vystřižení? 0,1x0,1? Nebo 0,01x0,01...?
Má kouzelná buřinka asi nefunguje.... Jinak bych tu nebyl...
Reputace slušností...
Předem všem děkuji za Vaše rady..
Offline
- (téma jako vyřešené označil(a) PanTau)
#2 08. 12. 2013 10:41
Re: Největší objem z obdélníku..
Ahoj ↑ PanTau:,
Podla udajov cvicenia hrany tvojej krabice
Budu
10-2x
5-2x
x
( pochopitelne 0<x<5 )
Napis aky objem ma potom tvoja krabica
Napr. vdaka hladaniu maxima objemu ako funkcie premennej x, vyjadri ho.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#3 08. 12. 2013 14:15
- kaja.marik
- Veterán
- Příspěvky: 1915
- Reputace: 57
Re: Největší objem z obdélníku..
Ale jaký je nejmenší možný čtverec vystřižení? 0,1x0,1? Nebo 0,01x0,01...?
Zalezi na tom, jake ma clovek nuzky, ale pro reseni ulohy nas to zajimat nemusi.
Offline
#4 09. 12. 2013 15:16
Re: Největší objem z obdélníku..
↑ PanTau:
Mohl bys mi prosimtě poradit, mam stejný příklad jen 4x8 ,spočetl sem V různými způsoby, potřebuju vědět, který je správný, poradil bys mi jestli si to vyřešil přesný postup jak si to vyřešil?
Děkuju
Offline
#5 09. 12. 2013 21:07
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Největší objem z obdélníku..
Zdravím,
cris11 napsal(a):
spočetl sem V různými způsoby,
možná by celému týmu prospělo se podělit alespoň o některý z nalezených způsobů. Děkuji.
Offline
#7 10. 12. 2013 10:27
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Největší objem z obdélníku..
↑ PanTau:
no tomu, co tady v tématu vznikl, ne?
K problému - v odkazovaném tématu (co cituješ) mám i odkaz na sbírku úloh - zkoušel jsi polistovat? Děkuji.
Offline
#8 10. 12. 2013 10:36 — Editoval PanTau (10. 12. 2013 10:38)
Re: Největší objem z obdélníku..
↑ jelena:
Samozřejmě, ale nenašel jsem tam nic co by mi mělo pomoct (nebo jsem to možná přehlédl, protože jsem nevěděl že právě to mi má pomoct).
↑ vanok:
vanok napsal(a):
Ahoj ↑ PanTau:,
Podla udajov cvicenia hrany tvojej krabice
Budu
10-2x
5-2x
x
( pochopitelne 0<x<5 )
Napis aky objem ma potom tvoja krabica
Napr. vdaka hladaniu maxima objemu ako funkcie premennej x, vyjadri ho.
f1(x) = 10-2x
f2(x) = 5-2x
f3(x) = x
Kdy x je na intervalu 0<x<5 , a z tich funkcí mám najít globální maximum?
Má kouzelná buřinka asi nefunguje.... Jinak bych tu nebyl...
Reputace slušností...
Předem všem děkuji za Vaše rady..
Offline
#9 10. 12. 2013 10:59
Re: Největší objem z obdélníku..
Ano, lebo objem je V(x)=(10-2x)(5-2x)x
Vdaka derivaci najdi kriticke body a over ci tak nenajdes maximum funkcie V.
Poznamka: pre geometricke dovody to x musi byt dokonca 0<x<2,5.(5-2xmusi byt kladne ako aj x).
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#10 10. 12. 2013 11:01 Příspěvek uživatele gladiator01 byl skryt uživatelem gladiator01.
#11 10. 12. 2013 12:47
Re: Největší objem z obdélníku..
↑ vanok:

Kritické body: 
Ano, našel jsem maximum funkce a to je: 

Má kouzelná buřinka asi nefunguje.... Jinak bych tu nebyl...
Reputace slušností...
Předem všem děkuji za Vaše rady..
Offline
#13 10. 12. 2013 19:14 — Editoval gladiator01 (10. 12. 2013 19:15)
- gladiator01


- Místo: Jindřichův Hradec
- Příspěvky: 1587
- Škola: ZČU FAV - SWI
- Pozice: absolvent
- Reputace: 53
- Web
Re: Největší objem z obdélníku..
↑ PanTau:
Dosadíš tu nezaokrouhlenou verzi do V(x)
Naděje jako svíce jas, potěší srdce štvané, čím temnější je noční čas, tím zářivěji plane.
VIVERE - MILITARE EST (Seneca)
Vím, že nic nevím. - Sokrates
Offline
#14 10. 12. 2013 20:17
Re: Největší objem z obdélníku..
↑ gladiator01:
Díky za radu, jen pro ujasnění, to co vyjde, je již největší objem?
http://www.wolframalpha.com/input/?i=%2 … %283%29%29
Má kouzelná buřinka asi nefunguje.... Jinak bych tu nebyl...
Reputace slušností...
Předem všem děkuji za Vaše rady..
Offline
#15 10. 12. 2013 20:31
Re: Největší objem z obdélníku..
↑ PanTau:
Vyborne, vidim, ze vies pouzit co som ti napisal.
Dobre pokracovanie.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#16 10. 12. 2013 23:24
Re: Největší objem z obdélníku..
Má kouzelná buřinka asi nefunguje.... Jinak bych tu nebyl...
Reputace slušností...
Předem všem děkuji za Vaše rady..
Offline
#17 10. 12. 2013 23:37
Re: Největší objem z obdélníku..
To ti jednoducho da hodnotu objemu V (x) v bode kde je maximalny. ( ako si to dokazal vdaka derivacii).
Mozes skusit vsetki ine hodnoty, na intervale kde problem ma zmysel su mensie... No je to zbytocne vdaka dokazu.
Srdecne Vanok
The respect, the politeness are essential qualities...and also the willingness.
Do not judge the other one.
Ak odpovedam na nejaku otazku. MOJ PRINCIP NIE JE DAT ODPOVED ALE UKAZAT AKO SA K ODPOVEDI DOSTAT
Offline
#18 11. 12. 2013 09:10
Re: Největší objem z obdélníku..
Dobrý den,
mám obdobný příklad akorát pro obdélníkový plech 4x8. Sbažil jsem se přijít na výsledek, tak bych prosil o ověření a popřípadě poradit.
f1=8-2x
f2=4-2x
f3=x
x tedy by mělo být na intervalu 0<x<2
Teď bych měl najít kritické body díky derivaci a maximum.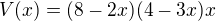


Pokud dosadím zpět do 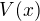 , tak pro první hodnotu vychází objem záporný, což nelze a druhý mi vyšel
, tak pro první hodnotu vychází objem záporný, což nelze a druhý mi vyšel 
Mohu prosit o překontrolování? Děkuji předem.
Offline
#19 11. 12. 2013 10:35
- jelena
- Jelena
- Místo: Opava
- Příspěvky: 30020
- Škola: MITHT (abs. 1986)
- Pozice: plním požadavky ostatních
- Reputace: 100
Re: Největší objem z obdélníku..
Zdravím v tématu,
↑ PanTau: v odkazu je to "Problém vnuka", ale celá práce stoji za pohlédnutí (jsou tam hezké obrázky).
↑ tesarin: proč v 2. závorce pro V je -3x?
↑ tesarin:, ↑ cris11: a další ze stejného vzdělávacího ústavu: navrhuji zpracovat pro obecné rozměry: máme obdélník o rozměrech m, n ( 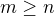 ), potom objem kvádru, co vznikne po vystřižení čtverců v rozích (strana čtverce
), potom objem kvádru, co vznikne po vystřižení čtverců v rozích (strana čtverce  ) bude
) bude  , tuto funkci jedné proměnné vyšetřujeme na maximum, přičemž budeme si dávat pozor na podmínky pro parametry
, tuto funkci jedné proměnné vyšetřujeme na maximum, přičemž budeme si dávat pozor na podmínky pro parametry  a výsledky výpočtu s ohledem na realitu situace.
a výsledky výpočtu s ohledem na realitu situace.
Zalezi na tom, jake ma clovek nuzky,
Vzhledem k tomu, že neumíme stříhat přibližně, ale pouze eukleidovsky sestrojitelné délky, výsledky výpočtů nezaokrouhlujeme, ale zapisujeme i s 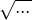 , pokud vynikne při výpočtu.
, pokud vynikne při výpočtu.
Offline
#21 11. 12. 2013 11:40 — Editoval Cheop (11. 12. 2013 12:39)
- Cheop


- Místo: okres Svitavy
- Příspěvky: 8209
- Škola: PEF VŠZ Brno (1979)
- Pozice: důchodce
- Reputace: 366
Re: Největší objem z obdélníku..
↑ tesarin:
Obecně:
Máme-li desku o stranách a, b a z ní máme v rozích odstřihnout čtverečky o straně x, tak abychom získali co největší objem, potom strana čtverečku bude: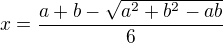
Maximální objem bude: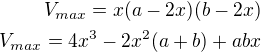
Nikdo není dokonalý
Offline
#22 11. 12. 2013 11:56
Re: Největší objem z obdélníku..
Děkuji všem zůčastněným za rady výsledek mého příkladu je zde: ↑ PanTau:
Největší objem : 
Má kouzelná buřinka asi nefunguje.... Jinak bych tu nebyl...
Reputace slušností...
Předem všem děkuji za Vaše rady..
Offline
