Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 17. 12. 2013 16:51
Pohyb sem a tam
Zítra píšeme test na tyto příklady: prosím vysvětlení a výpočet.
1) Z místa A vyjel v 8:00 hodin kamion rychlosti 60 kmh. Z místa B, které je od A vzdálené 225km, vyjelo proti němu osobní auto rychlostí 90 kmh. Urči, kdy a jak daleko od místa A se vozidla setkají.
2) Dan a Honza bydlí od sebe 4 km. Domluvili se, že se sejdou na cestě mezi oběma domovy. Dan vyšel ve 14 hodin rychlostí 5 kmh. Honza mu vyjel naproti na kole rychlostí 15 kmh. V kolik hodin se setkali a jakou vzdálenost ujel Honza?
Předem díky
Offline
#2 17. 12. 2013 16:57
Re: Pohyb sem a tam
Tak ještě jeden:
tady s tim si nevím vůbec rady
3) Vojta vyšel z domu ve tři hodiny odpoledne rychlostí 4 km/h. O půl hodiny později za ním ze stejného místa vyjel Filip na kole rychlostí 12 km/h. Za jak dlouho dohoní Filip Vojtu a jak daleko to bude od domu?
Řešíme to pomocí soustacy rovnic.. ale nevím jak je sestavit..
Offline
#3 17. 12. 2013 17:01 — Editoval xstudentíkx (17. 12. 2013 17:37)
- xstudentíkx


- Příspěvky: 962
- Škola: VŠE
- Pozice: student
- Reputace: 26
Re: Pohyb sem a tam
Ahoj
Napíšu ti pomocné body, dle kterých to určitě zvládneš ;)
1) v1=60 km/h v2=90 km/h
s1=v1*t1 s2=v2*t2
s=225=s1+s2
t1=t2 (jsou stejné, pojedou stejnou dobu)
Vypočítej čas (t)
Stačí sestavit jednoduchou rovnici.
Druhý příklad je na úplně stejným principu :)
Pokud nechápeš, tak řekni :)
U třetího je třeba si uvědomit, že se dohánějí, proto bude platit vztah s1=s2
Offline
#4 18. 12. 2013 06:52 — Editoval Cheop (18. 12. 2013 09:19)
- Cheop


- Místo: okres Svitavy
- Příspěvky: 8209
- Škola: PEF VŠZ Brno (1979)
- Pozice: důchodce
- Reputace: 366
Re: Pohyb sem a tam
↑ vojtaboh:
Pro př.3) bude platit: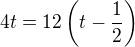 kde t je čas, který potřebuje Vojta
kde t je čas, který potřebuje Vojta
Ujetá vzdálenost je potom 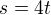
Nebo: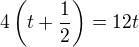 kde t je čas, který potřebuje Filip
kde t je čas, který potřebuje Filip
Ujetá vzdálenost je potom: 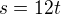
Nikdo není dokonalý
Offline
#5 19. 12. 2013 11:57 — Editoval greenic (19. 12. 2013 12:37)
Re: Pohyb sem a tam
↑ vojtaboh:
Vim, ze to mas resit soustavou, ale kazdopadne toto jsou velmi jednoduche priklady na uvahu:
1)
z A 60km/h a z B 90km/h proti sobe, maji vzdalenost 225 km... kolikrat se do toho vlezou oba, prvni cela cisla:
225 - 60 -60 -90 -90 = -75, to je moc, tkaze
225-60-90=75... takze oba ujedou za hodinu 60 a 90 km proti sobe a ted jsou proti sobe pouze 75 km
prvni ma rychlost 60 a druhy 90, kdyz si to podelis, mas pomer 2:3, 75:5=15 km, 15x2= 30 km a 15*3=45 km.
Ted to secteme, 60+30 = 90km ujede A
90+45 = 135 km ujede B
A ted cas, oba maji uz hodinu (odecetli jsme 60 a 90) a ted ten zbyly cas ktery bude pod hodinu,
A: 30 km ujel navic, ma 60km/h rychlost, to je polovina, takze 30 minut.
Jeli proti sobe, takze stejny cas.
Zaver : A ujel 90km a B 135 km a trvalo jim to hodinu a pul (vyjeli v 8, takze se setkali v 9:30)
2)
4 km mezi sebou, proti sobe, stejny cas, akorat jine rychlosti
D jede 5km/h a H 15 km/h, tudiz H jede 3x rychleji, pomer 1:3... 4km : 4(3+1 z pomeru)=1km (jeden dilek)
1x1= 1km ujde D , 3x1=3km ujede H
Vime kolik ujedou, ted uz jen cas, jelikoz jedou zaroven, tak bude stejny:
Dan: ujde 1km pri 5km/h... to je petina casu pri rychlosti, takze 60min:5 = 12minut
Zaver: Setkali se v 8:12 a Honza ujel 3 km.
3)
Ten uz je trosku slozitejsi diky rozdilnemu casu (jeden vysel driv), ale lehce si to prevedeme.
Vojta vyrazi v 15:00 a Filip v 15:30, V jde 4km/h a F jede 12km/h
To znamena, ze kdyz prave vyrazi na cestu F, tak V uz je pul hodiny na ceste. Pri jeho rychlosti 4km/h urazi za pul hodiny uz 2km.
Takze V uz usel 2 km (pri 4km/h) a F prave vyrazi s 12km/h, hledame v jake vzdalenosti se setkaji, logicky to bude pod hodinu, protoze jinak by F urazil 12km a to by bylo uz moc, takze pokracujem:
po pul hodine: V= 2km+ 2km (za pul hod zas urazi 2km pri 4km/h), F=6.... 4se nerovna 6, tkaze jeste min
ctvrt hodina: V= 2km + 1, F= 3 (ctvrtina z jeho rychlosti ) ... 3=3, mame vysledek
Zaver: F dohoni V za 15minut a budou 3km daleko od domu.
Offline
#6 02. 01. 2014 07:59
- petrik_ch

- Místo: Topoľčany
- Příspěvky: 242
- Škola: ZS Tribecska Topolcany
- Pozice: priatel skoly, absolvent, rodic
- Reputace: 2
- Web
Re: Pohyb sem a tam
Priklad 3: 15 min a 3 km - pekne aj s riesenim:
http://www.hackmath.net/cz/priklad/902
Offline