Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 16. 12. 2013 12:54
- vojta_vorel

- Příspěvky: 70
- Škola: MFF UK
- Pozice: student
- Reputace: 5
Re: -
Ahoj
Potřebujeme pomocí příslušných předpokladů dokázat dvě věci:
(1) 
(2) 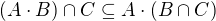
Tak začněme s tou první. Vezměme cokoli z  a ukažme, že to leží taky v
a ukažme, že to leží taky v 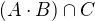 . Nějaký nápad, jak na to?
. Nějaký nápad, jak na to?
Offline
#3 16. 12. 2013 17:30 Příspěvek uživatele paha154 byl skryt uživatelem paha154. Důvod: FIN
#4 16. 12. 2013 20:45
- vojta_vorel

- Příspěvky: 70
- Škola: MFF UK
- Pozice: student
- Reputace: 5
Re: -
No, předpokládáme že A,B,C jsou podgrupy H a že 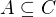 .
.
Z toho chceme vyvodit, že 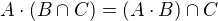
To je tvrzení o rovnosti dvou množin a takováhle tvrzení se typicky dokazují dvěma kroky. Že první je podmnožina druhé a že druhá je podmnožina první:
(1) 
(2) 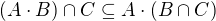
To je podle mě hodně důležitá představa. Nebo jsi zvyklý na nějakou jinou metodu? Dělali jste nějaké takové důkazy na cvičeních?
Offline
#5 16. 12. 2013 21:25 Příspěvek uživatele paha154 byl skryt uživatelem paha154. Důvod: FIN
#6 16. 12. 2013 21:54 Příspěvek uživatele paha154 byl skryt uživatelem paha154. Důvod: FIN
#7 17. 12. 2013 08:14
- vojta_vorel

- Příspěvky: 70
- Škola: MFF UK
- Pozice: student
- Reputace: 5
Re: -
No tak vezmem tu první. Berem prvek z 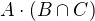 a chcem ukázat, že je v
a chcem ukázat, že je v 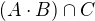 . Co znamená, řečeno slovy, že něco leží v
. Co znamená, řečeno slovy, že něco leží v 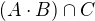 , tedy v průniku nějakých dvou množin?
, tedy v průniku nějakých dvou množin?
Offline
#8 17. 12. 2013 14:16 Příspěvek uživatele paha154 byl skryt uživatelem paha154. Důvod: FIN
#9 17. 12. 2013 17:45
- vojta_vorel

- Příspěvky: 70
- Škola: MFF UK
- Pozice: student
- Reputace: 5
Re: -
Přesně tak. Tak se ještě jednou zkus pořádně zamyslet, jestli nevymyslíš, proč za daných předpokladů musí vše z 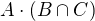 ležet v
ležet v 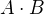 a taky v
a taky v  .
.
Offline
#10 17. 12. 2013 17:47 Příspěvek uživatele paha154 byl skryt uživatelem paha154. Důvod: FIN
#11 17. 12. 2013 18:52
- vojta_vorel

- Příspěvky: 70
- Škola: MFF UK
- Pozice: student
- Reputace: 5
Re: -
No, tak to bude patrně jádro problému. To krát funguje následovně. Když máme dvě množiny v nějké grupě s operací  (třeba to můžou být podgrupy
(třeba to můžou být podgrupy 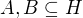 ), tak jejich součin
), tak jejich součin 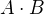 vznikne tak, že vezmu všechny násobky tvaru
vznikne tak, že vezmu všechny násobky tvaru 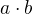 kde
kde  , tedy
, tedy
Zkus si to představit třeba s reálnými čísly. Rozmysli si třeba, co to je 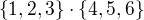
Offline
#12 17. 12. 2013 18:56 Příspěvek uživatele paha154 byl skryt uživatelem paha154. Důvod: FIN
#13 18. 12. 2013 08:01
- vojta_vorel

- Příspěvky: 70
- Škola: MFF UK
- Pozice: student
- Reputace: 5
Re: -
Přesně tak. No, a až si aspoň trochu osvojíš tuhle myšlenku, musí podle mě být docela lehké si rozmyslet, že platí náš bod (1), tedy že pokud 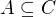 , musí:
, musí:
(1a) vše z 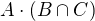 ležet v
ležet v 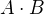
(1b) vše z 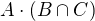 ležet v
ležet v  .
.
Nezapomeň na jasný fakt, že 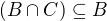 a
a 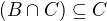 !
!
Offline
#14 18. 12. 2013 14:06 Příspěvek uživatele paha154 byl skryt uživatelem paha154. Důvod: FIN
#15 19. 12. 2013 08:11
- vojta_vorel

- Příspěvky: 70
- Škola: MFF UK
- Pozice: student
- Reputace: 5
Re: -
To proto, že C je podgrupa. Proto součin dvou věcí z C je opět v C.
Offline