Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 28. 04. 2012 09:56 — Editoval wolfito (28. 04. 2012 10:04)
Re: Kolmost vektorů
Ahoj, navedu tě.
Spočítej si směrový vektor z bodu A a B přímky p:  jak určitě víš tak ze směrového vektoru se dělá normalový vektor a normalovy vektor je kolmy k přímce.
jak určitě víš tak ze směrového vektoru se dělá normalový vektor a normalovy vektor je kolmy k přímce.
Ještě nám chybí spočítat cečko. To je tak když máš přímku  , tedy za bod
, tedy za bod  a
a  dame souřadnice bodu A nebo B a za
dame souřadnice bodu A nebo B a za  a
a  dame normalovy souřadnice.
dame normalovy souřadnice.
Radost z uvažování a z chápání je nejkrásnějším darem přírody.
Offline
#3 28. 04. 2012 10:42 Příspěvek uživatele TerezaH byl skryt uživatelem TerezaH.
#5 30. 04. 2012 17:52
Re: Kolmost vektorů
↑ TerezaH:
Dobrý den,
vypočtěte směrový vektor přímky p:  .
.
Normálový vektor hledané přímky pak bude mít souřadnice:  kde
kde  .
.
Z toho pro 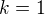 již je přímo vidět výsledek.
již je přímo vidět výsledek.
Offline
#6 02. 05. 2012 19:12
Re: Kolmost vektorů
Takjo napsal(a):
↑ TerezaH:
Dobrý den,
vypočtěte směrový vektor přímky p:.
Normálový vektor hledané přímky pak bude mít souřadnice:kde
.
Z toho projiž je přímo vidět výsledek.
Dobrý den, mohl byste mi trochu osvětlit vaše řešení?
Pokud mám směrový vektor  tak normálový vektor musí být přece
tak normálový vektor musí být přece  nebo
nebo  , ale pak mi to nesedí s řešením E. I když vím, že je to podle výsledků správná odpověď. Díky za radu.
, ale pak mi to nesedí s řešením E. I když vím, že je to podle výsledků správná odpověď. Díky za radu.
Offline
#7 02. 05. 2012 19:38
Re: Kolmost vektorů
↑ And777:
Dobrý den,
normálový vektor přímky p vůbec nepočítejte, je to ztráta času.
Stačí si uvědomit, že pokud jsou dvě přímky na sebe kolmé a jedna z nich je vyjádřena směrovým vektorem
a druhá normálovým vektorem, pak jsou oba vektory rovnoběžné, přesněji, jeden je nenulovým násobkem druhého.
Nakreslete si obrázek a pochopíte... :)
Offline
#9 02. 05. 2012 19:58 — Editoval Takjo (02. 05. 2012 20:20)
Re: Kolmost vektorů
↑ wolfito:
Dobrý den,
váš postup rozhodně není špatný, ale poněkud zdlouhavý, protože příklad chce jenom zjistit, zda jsou přímky na sebe kolmé a ne jejich rovnice.
Jiné by to bylo kdyby mezi možnými výsledky byly dvě přímky, které by měly stejné normálové vektory (nebo jejich nenulové násobky) a lišily by se pouze absolutním členem.
Pak by byl váš postup nezbytný... :)
Úloha by pak zněla: najděte přímku, která je kolmá na přímku p a prochází bodem např. A.
Offline
#10 02. 05. 2012 20:09
Re: Kolmost vektorů
Takjo napsal(a):
↑ And777:
Dobrý den,
normálový vektor přímky p vůbec nepočítejte, je to ztráta času.
Stačí si uvědomit, že pokud jsou dvě přímky na sebe kolmé a jedna z nich je vyjádřena směrovým vektorem
a druhá normálovým vektorem, pak jsou oba vektory rovnoběžné, přesněji, jeden je nenulovým násobkem druhého.
Nakreslete si obrázek a pochopíte... :)
Jsem já to ale jelito :-) díky, vždyť je to úplně primitivní.
Offline
#11 18. 12. 2013 16:40
Re: Kolmost vektorů
Ahoj, věřím, že to bude jednoduché , ale nemůžu v tom najít logiku. Našel by se někdo, kdo by podrobněji vysvětlil ?
Chápu jen směrový vektor (-6;-4) ...proč je ale najednou (3;2) ? .... jak pak prokázat kolmost s ohledem na dané rovnice přímky ?díky moc
Offline
#12 18. 12. 2013 17:24
Re: Kolmost vektorů
↑ Drat:
Dobrý den,
každá přímka má nekonečně mnoho směrových (i normálových) vektorů, neboť je-li nějaký vektor nenulovým násobkem jiného vektoru,
pak jsou oba tyto vektory rovnoběžné.
V našem příkladu platí:  ;
; 
Offline

