Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#3 01. 01. 2014 14:48
Re: komplexní čísla - podíl
↑ aferon:
Není. Proč tam máš 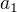 a
a  ? To je zbytečné.
? To je zbytečné.
120° je vlastně  . Tabulka uvádí jen
. Tabulka uvádí jen 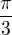 , tak vezmeš tabulkovou hodnotu pro sinus a kosinus a každou z nich vynásobíš dvěma a dostaneš tím hodnotu pro
, tak vezmeš tabulkovou hodnotu pro sinus a kosinus a každou z nich vynásobíš dvěma a dostaneš tím hodnotu pro 
Kosinus bude -1, protože ten úhel sahá do druhého kvadrantu a tam je kosinus záporný.
Sinus bude 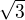 , protože ve druhém kvadrantu je sinus kladný. Tím dostáváš:
, protože ve druhém kvadrantu je sinus kladný. Tím dostáváš:
 To je algebraický tvar toho čísla
To je algebraický tvar toho čísla  .
.
A teď vydělíš:
Offline
#7 01. 01. 2014 15:34
Re: komplexní čísla - podíl
↑ aferon:
To s tím asi nemá moc společného. To "a" v tom vzorečku tam má jen zástupný charakter podle mě za reálnou složku komplexního čísla, a "b" zase za imaginární složku toho komplexního čísla.
A v zadání je "a" označení celého komplexního čísla, jen to číslo je v goniometrickém tvaru, a "b" je zase druhé komplexní číslo jen v algebraickém tvaru. To je třeba umět rozlišit.
Offline
#8 01. 01. 2014 15:49 — Editoval aferon (01. 01. 2014 15:53)
Re: komplexní čísla - podíl
↑ bejf:
↑ bejf:
tak to taky chápu a nejdřív jsem chtěl pracovat s komplexními čísly pouze v algebraickém tvaru, tak jsem si číslo "a" převedl z gon. tvaru na algebraický tvar
a jak jste tady převáděl úhly na základní, tak kalkulačka mně vždy vrátí stejnou hodnotu
tady sem našel příklad:
takže pro tenhle konkrétní příklad by člen "a" měl být a=
Offline
#9 01. 01. 2014 16:02
Re: komplexní čísla - podíl
↑ aferon:
Jenže pleteš jabka s hruškama. To áčko v tom posledním příkladě (a taky v zadání toho tvého prvního příkladu) je CELÉ komplexní číslo, kdežto na vzoreček co ses odvolával, tak tam to áčko je JEN reálná část.
Navíc v tom tvém výpočtu nikde není vidět, že bys tam  a
a  vůbec měl.
vůbec měl.
Offline
#10 01. 01. 2014 16:07 — Editoval aferon (01. 01. 2014 16:12)
Re: komplexní čísla - podíl
↑ bejf:
vždyť ano  je reálná část
je reálná část je imaginární část
je imaginární část
a číslo "a" a číslo"b" tvoří celé imaginární číslo
a tady v tom mém nepřehledném zapsání
je a1 reálná část a2 je imaginární část
pouze jsem chtěl převést celé imaginární číslo "a" a=3(cos 120 +sin120) na algebraický tvar
Offline







 a ty máš úhel
a ty máš úhel  proč je tato hodnota špatně?
proč je tato hodnota špatně?
