Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 10. 01. 2014 19:46
Lokální a globální extrémy
Potřebovala bych poradit jak najít lokální a globální extrémy.
Fce f(t) = t + 2/t na intervalu I= (-5,5)
Vím že nejpreve se fce derivuje a co poté ? jak zjistím ty minima a maxima ?? Potřebovala bych poradit s postupem jak to vyřešit ... Předem díky ..
Offline
#2 10. 01. 2014 20:10
Re: Lokální a globální extrémy
Když položíš derivaci funkce nule, zjistíš v jakých bodech je tečna v daných bodech rovnoběžná s osou x. Čili to jinými slovy znamená, že tam je buď maximum nebo minimum (bud absolutní nebo lokální).
Zde máš: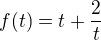
derivace jednoduše: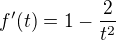
Takže ji položíš nule: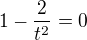
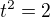
Čili tečna rovnoběžná s osou x bude v bodech 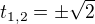
Teď stačí jen dosadit do původní rovnice a zjistíš jestli je to minimum nebo maximum
L'Hospitalovo pravidlo neexistuje. Byl to výsledek Johanna Bernoulliho
Offline
#4 11. 01. 2014 10:03
Re: Lokální a globální extrémy
Interval 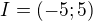 je pouze intervalem, na kterém ty lokální extrémy máš hledat. Na tomto intervalu jsou zároveň i 2 globální extrémy (z celkových 4). Jenže ty hledáš lokální extrémy, čili místo, kde je tečna k dané funkci rovnoběžná s osou x
je pouze intervalem, na kterém ty lokální extrémy máš hledat. Na tomto intervalu jsou zároveň i 2 globální extrémy (z celkových 4). Jenže ty hledáš lokální extrémy, čili místo, kde je tečna k dané funkci rovnoběžná s osou x
L'Hospitalovo pravidlo neexistuje. Byl to výsledek Johanna Bernoulliho
Offline
