Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#1 19. 01. 2014 12:15
Křivkový integrál
Ahoj, zasekla jsem se na jednoduchém příkladě.. Můžete mě prosím někdo popostrčit? Zadání:  , K je graf funkce y = ln x na intervalu <1,2>. Mám vypočítat křivkový integrál 1.druhu. Parametrizovala jsem x = t, y = ln t,
, K je graf funkce y = ln x na intervalu <1,2>. Mám vypočítat křivkový integrál 1.druhu. Parametrizovala jsem x = t, y = ln t,  , dx = 1 dt, dy = (1/t) dt. Počítala jsem integrál takto:
, dx = 1 dt, dy = (1/t) dt. Počítala jsem integrál takto: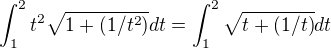 No a teď nemůžu přijít na to, jakou substituci použít.. Když napíšu primitivní funkci rovnou, dělila bych nulou.
No a teď nemůžu přijít na to, jakou substituci použít.. Když napíšu primitivní funkci rovnou, dělila bych nulou.
Offline
- (téma jako vyřešené označil(a) nanny1)