Matematické Fórum
Nevíte-li si rady s jakýmkoliv matematickým problémem, toto místo je pro vás jako dělané.
Nástěnka
❗22. 8. 2021 (L) Přecházíme zpět na doménu forum.matweb.cz!
❗04.11.2016 (Jel.) Čtete, prosím, před vložení dotazu, děkuji!
❗23.10.2013 (Jel.) Zkuste před zadáním dotazu použít některý z online-nástrojů, konzultovat použití můžete v sekci CAS.
Nejste přihlášen(a). Přihlásit
#2 29. 01. 2009 14:49
Re: Binomická věta
↑ Lucas456:
Asi snad iba vediet pocitat mocniny a kombinacne cisla, resp. mat dobru kalkulacku :))
Dobrou pomockou je aj Pascalov trojuholnik, pretoze koeficienty pri jednotlivych clenoch rozkladu podla binomickej vety, su koeficientami n-teho riadku Pascalovho trojuholnika (pricom sa zacina cislovat od nuly) ked upravujes nejaky vyraz  :)
:)
Offline
#3 29. 01. 2009 14:56 — Editoval Cheop (29. 01. 2009 14:56)
- Cheop


- Místo: okres Svitavy
- Příspěvky: 8209
- Škola: PEF VŠZ Brno (1979)
- Pozice: důchodce
- Reputace: 366
Re: Binomická věta
↑ Lucas456:
Snad jen doplním ke kombinačním číslům.
Vhodné je používat tento vztah: 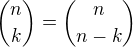
Nikdo není dokonalý
Offline
#4 29. 01. 2009 15:03
Re: Binomická věta
↑ Cheop:
Ano, dokonca priamo z Pascalovho trojuholnika vidno este dalsie vztahy, napriklad ze 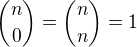 ,
, 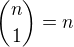 alebo z toho, ze v Pascalovom trojuholniku sucet dvoch cisel sa rovna cislu umiestnemu pod nimi, plati vztah
alebo z toho, ze v Pascalovom trojuholniku sucet dvoch cisel sa rovna cislu umiestnemu pod nimi, plati vztah 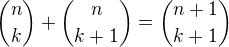 . Dobra pomocka ten trojuholnik, no nie? :)
. Dobra pomocka ten trojuholnik, no nie? :)
Offline
#6 29. 01. 2009 17:33
Offline


